
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,![]() )三点.
)三点.

(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
【答案】解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
∵A(﹣1,0),B(5,0),C(0,![]() )三点在抛物线上,
)三点在抛物线上,
∴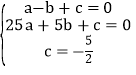 ,解得
,解得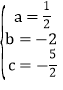 。
。
∴抛物线的解析式为:![]() 。
。
(2)∵![]() ,∴其对称轴为直线x=2。
,∴其对称轴为直线x=2。
连接BC,如图1所示,
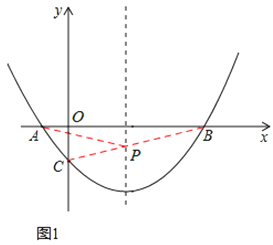
∵B(5,0),C(0,![]() ),
),
∴设直线BC的解析式为y=kx+b(k≠0),
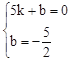 ,解得:
,解得: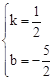 。
。
∴直线BC的解析式为![]() 。
。
当x=2时,![]() ,
,
∴P(2,![]() )。
)。
(3)存在。
如图2所示,
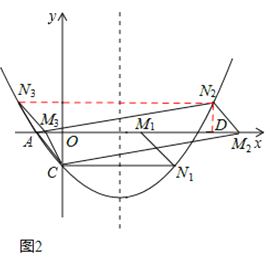
①当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C(0,![]() ),
),
∴N1(4,![]() )。
)。
②当点N在x轴上方时,
如图2,过点N作ND⊥x轴于点D,
在△AND与△MCO中, ,
,
∴△AND≌△MCO(ASA)。
∴ND=OC=![]() ,即N点的纵坐标为
,即N点的纵坐标为![]() 。
。
∴![]() ,解得
,解得![]() 或
或![]() 。
。
∴N2(![]() ,
,![]() ),N3(
),N3(![]() ,
,![]() ).
).
综上所述,符合条件的点N的坐标为(4,![]() ),(
),(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
试题本题考查的是二次函数综合题,涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识,在解答(3)时要注意进行分类讨论.(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(﹣1,0),B(5,0),C(0,![]() )三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
)三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),∵A(﹣1,0),B(5,0),C(0,![]() )三点在抛物线上,∴
)三点在抛物线上,∴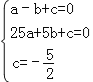 ,解得
,解得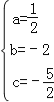 .∴抛物线的解析式为:y=
.∴抛物线的解析式为:y=![]() x2﹣2x﹣
x2﹣2x﹣![]() ;
;
(2)∵抛物线的解析式为:y=![]() x2﹣2x﹣
x2﹣2x﹣![]() ,∴其对称轴为直线x=﹣
,∴其对称轴为直线x=﹣![]() =﹣
=﹣![]() =2,连接BC,如图1所示,
=2,连接BC,如图1所示,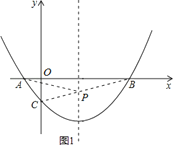
∵B(5,0),C(0,﹣![]() ),∴设直线BC的解析式为y=kx+b(k≠0),∴
),∴设直线BC的解析式为y=kx+b(k≠0),∴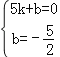 ,解得
,解得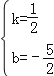 ,∴直线BC的解析式为y=
,∴直线BC的解析式为y=![]() x﹣
x﹣![]() ,当x=2时,y=1﹣
,当x=2时,y=1﹣![]() =﹣
=﹣![]() ,∴P(2,﹣
,∴P(2,﹣![]() );
);
(3)存在.如图2所示,
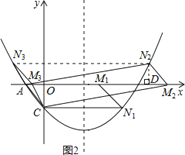
①当点N在x轴下方时,∵抛物线的对称轴为直线x=2,C(0,﹣![]() ),∴N1(4,﹣
),∴N1(4,﹣![]() );
);
②当点N在x轴上方时,如图2,过点N2作N2D⊥x轴于点D,在△AN2D与△M2CO中,
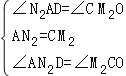 ∴△AN2D≌△M2CO(ASA),∴N2D=OC=
∴△AN2D≌△M2CO(ASA),∴N2D=OC=![]() ,即N2点的纵坐标为
,即N2点的纵坐标为![]() .∴
.∴![]() x2﹣2x﹣
x2﹣2x﹣![]() =
=![]() ,
,
解得x=2+![]() 或x=2﹣
或x=2﹣![]() ,∴N2(2+
,∴N2(2+![]() ,
,![]() ),N3(2﹣
),N3(2﹣![]() ,
,![]() ).综上所述,符合条件的点N的坐标为N1(4,﹣
).综上所述,符合条件的点N的坐标为N1(4,﹣![]() ),N2(2+
),N2(2+![]() ,
,![]() )或N3(2﹣
)或N3(2﹣![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.

(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:两个二次项系数之和为1,对称轴相同,且图象与y轴交点也相同的二次函数互为友好同轴二次函数![]() 例如:
例如:![]() 的友好同轴二次函数为
的友好同轴二次函数为![]() .
.
![]() 请你分别写出
请你分别写出![]() ,
,![]() 的友好同轴二次函数;
的友好同轴二次函数;
![]() 满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?
满足什么条件的二次函数没有友好同轴二次函数?满足什么条件的二次函数的友好同轴二次函数是它本身?
![]() 如图,二次函数
如图,二次函数![]() :
:![]() 与其友好同轴二次函数
与其友好同轴二次函数![]() 都与y轴交于点A,点B、C分别在
都与y轴交于点A,点B、C分别在![]() 、
、![]() 上,点B,C的横坐标均为
上,点B,C的横坐标均为![]() ,它们关于
,它们关于![]() 的对称轴的对称点分别为
的对称轴的对称点分别为![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,CB.
,CB.
![]() 若
若![]() ,且四边形
,且四边形![]() 为正方形,求m的值;
为正方形,求m的值;
![]() 若
若![]() ,且四边形
,且四边形![]() 的邻边之比为1:2,直接写出a的值.
的邻边之比为1:2,直接写出a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上午8时,一条船从海岛A出发,以15海里/时的速度向正北航行,10时到达海岛B处,从A,B望灯塔C,测得∠NAC=30,∠NBC=60.

(1)求从海岛B到灯塔C的距离;
(2)这条船继续向正北航行,问在上午或下午的什么时间小船与灯塔C的距离最短?
查看答案和解析>>
科目:初中数学 来源: 题型:
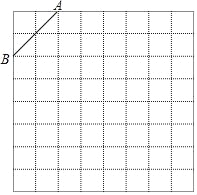
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ;
(3)求△ABC中BC边上的高长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 C 为线段 AB 上一点,△ACM、△CBN 都是等边三角形,AN、MC 交于点 E,BM、CN 交于点 F
(1)说明 AN=MB 的理由
(2)△CEF 是什么三角形?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com