
【题目】如图,点 C 为线段 AB 上一点,△ACM、△CBN 都是等边三角形,AN、MC 交于点 E,BM、CN 交于点 F
(1)说明 AN=MB 的理由
(2)△CEF 是什么三角形?为什么?

【答案】(1)见详解;(2)△CEF是等边三角形,理由见详解.
【解析】
(1)等边三角形的性质可以得出△ACN,△MCB两边及其夹角分别对应相等,两个三角形全等,得出线段AN与线段BM相等.
(2)平角的定义得出∠MCN=60°,通过证明△ACE≌△MCF得出CE=CF,根据等边三角形的判定得出△CEF的形状.
(1)证明:∵△ACM与△CBN都是等边三角形,
∴AC=MC,CN=CB,∠ACM=∠BCN=60°.
∴∠MCN=180°-∠ACM-∠BCN =60°,∠ACM+∠MCN=∠BCN+∠MCN,
即:∠ACN=∠MCB,
在△ACN和△MCB中
 ,
,
∴△ACN≌△MCB(SAS).
∴AN=BM.
(2)解:△CEF 是等边三角形,理由如下:
∵∠ACM═60°,∠MCN=60°,
∴∠ACM=∠MCN,
∵△ACN≌△MCB,
∴∠CAE=∠CMB.
在△ACE和△MCF中
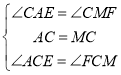
∴△ACE≌△MCF(ASA).
∴CE=CF.
又∵∠MCN=60°,
∴△CEF的形状是等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,![]() )三点.
)三点.

(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解本校七年级学生期末考试数学成绩情况,决定进行抽样分析已知该校七年级共有10个班,每班40名学生,请根据要求回答下列问题:
(1)若要从全年级学生中抽取一个40人的样本,你认为以下抽样方法中比较合理的有__________.(只要填写序号).
①随机抽取一个班级的学生;
②在全年级学生中随机抽取40名男学生;
③在全年级10个班中各随机抽取4名学生.
(2)将抽取的40名学生的数学成绩进行分组,并绘制频数表和成绩分布统计图(不完整),如图:
①请补充完整频数表;
成绩(分) | 频数 | 频率 |
| __________ | 0.3 |
| __________ | 0.4 |
| 8 | __________ |
| 4 | __________ |
②写出图中![]() 、
、![]() 类圆心角度数;并估计全年级
类圆心角度数;并估计全年级![]() 、
、![]() 类学生大约人数.
类学生大约人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC.

(1)如果∠B+∠C=120°,则∠AED的度数=______.(直接写出结果)
(2)根据⑴的结论,猜想∠B+∠C与∠AED之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
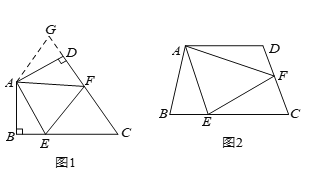
【题目】如图(![]() ),在四边形
),在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() .探究图中线段
.探究图中线段![]() ,
,![]() ,
,![]() 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,先证明
,先证明![]() ≌
≌![]() ,再证明
,再证明![]() ≌
≌![]() ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.
如图(![]() ),若在四边形
),若在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无锡市灵山胜境公司厂生产一种新的大佛纪念品,每件纪念品制造成本为18元,试销过程发现,每月销量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间的关系可以近似地看作一次函数
之间的关系可以近似地看作一次函数![]() .
.
![]() 写出公司每月的利润
写出公司每月的利润![]() 万元
万元![]() 与销售单价
与销售单价![]() 元
元![]() 之间函数解析式;
之间函数解析式;
![]() 当销售单价为多少元时,公司每月能够获得最大利润?最大利润是多少?
当销售单价为多少元时,公司每月能够获得最大利润?最大利润是多少?
![]() 根据工商部门规定,这种纪念品的销售单价不得高于32元
根据工商部门规定,这种纪念品的销售单价不得高于32元![]() 如果公司要获得每月不低于350万元的利润,那么制造这种纪念品每月的最低制造成本需要多少万元?
如果公司要获得每月不低于350万元的利润,那么制造这种纪念品每月的最低制造成本需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com