练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△ABC中，∠ACB＝90°，⊙O是△ABC的内切圆，三个切点分别为D、E、F，若BF＝2，AF＝3，则△ABC的面积是

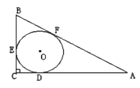
    A.6B.7C.D.12

    【答案】A

    【解析】

    利用切线的性质以及正方形的判定方法得出四边形OECD是正方形，进而利用勾股定理得出答案．

    连接DO，EO，

    ∵⊙O是△ABC的内切圆，切点分别为D，E，F，

    ∴OE⊥AC，OD⊥BC，CD=CE，BD=BF=3，AF=AE=4

    又∵∠C=90°，

    ∴四边形OECD是矩形，

    又∵EO=DO，

    ∴矩形OECD是正方形，

    设EO=x，

    则EC=CD=x，

    在Rt△ABC中

    BC2+AC2=AB2

    故（x+2）2+（x+3）2=52，

    解得：x=1，

    ∴BC=3，AC=4，

    ∴S△ABC=×3×4=6，

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若实数a，b满足a+b＝1时，就称点P（a，b）为“平衡点”．

    （1）判断点A（3，﹣4）、B（-1，2-）是不是平衡点；

    （2）已知抛物线y＝x2+（p﹣t﹣1）x+q+t﹣3（t＞3）上有且只有一个“平衡点”，且当﹣2≤p≤3时，q的最小值为t，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在某一时刻测得1米长的竹竿竖直放置时影长1.2米，在同一时刻旗杆AB的影长不全落在水平地面上，有一部分落在楼房的墙上，他测得落在地面上影长为BD＝9.6米，留在墙上的影长CD＝2米，则旗杆的高度（　　）

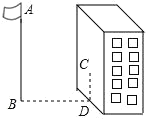
    A.9米B.9.6米C.10米D.10.2米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C、D在线段AB上，且△PCD是等边三角形.∠APB=120°.

    (1)求证：△ACP∽△PDB；

    (2)证明：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点在的直径的延长线上，点在上，且AC=CD，∠ACD=120°.

    （1）求证：是的切线；

    （2）若的半径为2，求图中阴影部分的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是正方形，E，F分别是DC和CB的延长线上的点，且BF＝DE，连接AE，AF，EF.

    （1）判断△ABF与△ADE有怎样的关系，并说明理由；

    （2）求∠EAF的度数,写出△ABF可以由△ADE经过怎样的图形变换得到；

    （3）若BC＝6，DE＝2，求△AEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

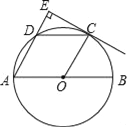
    【题目】如图，AB是⊙O的直径，点C、D为半圆O的三等分点，过点C作CE⊥AD，交AD的延长线于点E．

    （1）求证：CE为⊙O的切线；

    （2）判断四边形AOCD的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同．

    （1）若他去买一瓶饮料，则他买到奶汁的概率是 ；

    （2）若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶汁的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图

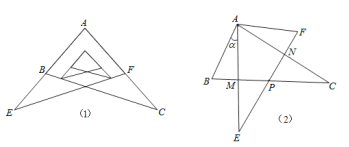
    （1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．

    （1）求证：AM=AN；

    （2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．

    查看答案和解析>>

    同步练习册答案