
【题目】如图,在△ABC中,∠ACB=90°,点O在AC上,以O为圆心,OC为半径作⊙O,过点A作AD⊥BO交BO的延长线于点D.则下列结论中:①点A、B、C、D在同一个圆上;②∠ABC=2∠CAD;③若∠BOC=∠BAD,则AB与⊙O相切,正确的结论是( )
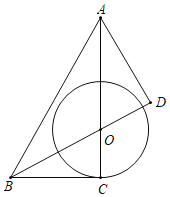
A.①②③B.①②C.②③D.①③
【答案】D
【解析】
由∠D=90°=∠ACB,得出点A、B、C、D在同一个圆上,①正确;证出∠OBC=∠CAD,当BD是∠ABC平分线时,∠ABC=2∠CAD,②错误;若∠BOC=∠BAD,则∠OBC=∠ABD,作OE⊥AB于E,由角平分线性质得出OE=OC,得出AB与⊙O相切,③正确;即可得出结论.
解:∵AD⊥BO,
∴∠D=90°=∠ACB,
∴点A、B、C、D在同一个圆上,①正确;
∵∠ACB=∠D=90°,∠BOC=∠AOD,
∴∠OBC=∠CAD,
当BD是∠ABC平分线时,∠ABC=2∠CAD,②错误;
若∠BOC=∠BAD,
∵∠ACB=∠D=90°,
∴∠OBC=∠ABD,
作OE⊥AB于E,如图所示:
则OE=OC,
∴AB与⊙O相切,③正确;
故选:D.


科目:初中数学 来源: 题型:
【题目】某商场为了吸引更多的顾客,安排了一个抽奖活动,并规定:顾客每购买100元商品,就能获得一次抽奖的机会.抽奖规则如下:在抽奖箱内,有100个牌子,分别写有1,2,3,…,100共100个数字,抽到末位数是5的可获20元购物券,抽到数字是88的可获200元购物券,抽到66或99的可获100元购物券.某顾客购物用了130元,他获得购物券的概率是多少?他获得20元、100元、200元购物券的概率分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
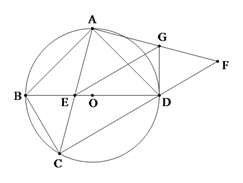
(1)证明:AC=AF;
(2)若AD=2,AF=![]() ,求AE的长;
,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=(x-2)2与x轴交于点A,与y轴交于点B,过点B作BC∥x轴,交抛物线于点C,过点A作AD∥y轴,交BC于点D,点P在BC下方的抛物线上(不与点B,C重合),连接PC,PD,设△PCD的面积为S,则S的最大值是________。
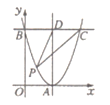
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂长
的等腰直角三角形,摆动臂长![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
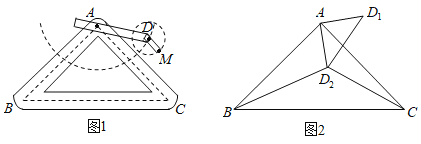
(1)在旋转过程中:
①当![]() 三点在同一直线上时,求
三点在同一直线上时,求![]() 的长;
的长;
②当![]() 三点在同一直角三角形的顶点时,求
三点在同一直角三角形的顶点时,求![]() 的长.
的长.
(2)若摆动臂![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块斜边长相等的等腰直角三角板按如图①摆放,斜边AB分别交CD,CE于M,N点.
(1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,如图②,求证:△CMF≌△CMN;
(2)将△CED绕点C旋转,则:
①当点M,N在AB上(不与点A,B重合)时,线段AM,MN,NB之间有一个不变的关系式,请你写出这个关系式,并说明理由;
②当点M在AB上,点N在AB的延长线上(如图③)时,①中的关系式是否仍然成立?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是甲、乙两校男、女生人数的统计图.
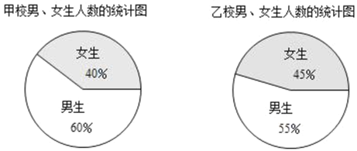
根据统计图回答问题:
(1)若甲校男生人数为273人,求该校女生人数;
(2)方方同学说:“因为甲校女生人数占全校人数的40%,而乙校女生人数占全校人数的55%,所以甲校的女生人数比乙校女生人数少”,你认为方方同学说的对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴分别于点A(﹣3,0),B(1,0),交y轴正半轴于点D,抛物线顶点为C.下列结论
①2a﹣b=0;
②a+b+c=0;
③当m≠﹣1时,a﹣b>am2+bm;
④当△ABC是等腰直角三角形时,a=![]() ;
;
⑤若D(0,3),则抛物线的对称轴直线x=﹣1上的动点P与B、D两点围成的△PBD周长最小值为3![]() ,其中,正确的个数为( )
,其中,正确的个数为( )
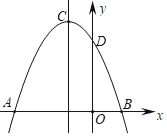
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=ax+b的图象上有两点A、B,它们的横坐标分别是3,-1,若二次函数y=![]() x2的图象经过A、B两点.
x2的图象经过A、B两点.
(1)请求出一次函数的表达式;
(2)设二次函数的顶点为C,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com