
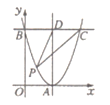
【题目】如图,在平面直角坐标系中,抛物线y=(x-2)2与x轴交于点A,与y轴交于点B,过点B作BC∥x轴,交抛物线于点C,过点A作AD∥y轴,交BC于点D,点P在BC下方的抛物线上(不与点B,C重合),连接PC,PD,设△PCD的面积为S,则S的最大值是________。
【答案】4
【解析】
根据抛物线的解析式求得A、B的坐标,和对称轴方程,根据BC∥x轴,AD∥y轴对称B、C是抛物线上的对称点,所以BD=DC=2,因为顶点A到直线BC的距离最大,所以点P与A重合时,△PCD面积最大,最大值为![]() DCAD=
DCAD=![]() ×2×4=4.
×2×4=4.
∵抛物线y=(x2)2与x轴交于点A,与y轴交于点B.
∴A(2,0),B(0,4),
∵抛物线y=(x2)2与的对称轴为x=2,BC∥x轴,AD∥y轴,
∴直线AD就是抛物线y=(x2)2与的对称轴,
∴B、C关于直线BD对称,
∴BD=DC=2,
∵顶点A到直线BC的距离最大,
∴点P与A重合时,△PCD面积最大,最大值为![]() DCAD=
DCAD=![]() ×2×4=4.
×2×4=4.
故最大值为4.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x-3,下列说法中正确的是( )
A.该函数图象的开口向下B.该函数图象的顶点坐标是(-2,-7)
C.当x<0时,y随x的增大而增大D.该函数图象与x轴有两个不同的交点,且分布在坐标原点两侧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泉州市旅游资源丰富,①清源山、②开元寺、③崇武古城三个景区是人们节假日玩的热点景区,张老师对八(1)班学生“五·一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别:A、游三个景区;B,游两个景区;C,游一个景区:D,不到这三个景区游玩现根据调查结果绘制了不完整的条形统计图和廟形统计图,请结合图中信息解答下列问题:
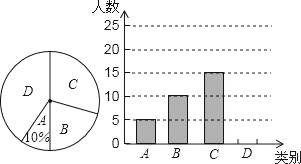
(1)八(1)班共有学生 人在扇形统计图中,表示“B类别的扇形的圆心角的度数为 ;
(2)请将条形统计图补充完整;
(3)若小华、小刚两名同学,各自从三个最区中随机选一个作为5月1日游玩的景区,请用树状图或列表法求他们选中同个景区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB和DE直立在地面上的两根立柱,已知AB=5m,某一时刻AB在太阳光下的影子长BC=3m.
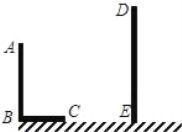
(1)在图中画出此时DE在太阳光下的影子EF;
(2)在测量AB影子长时,同时测量出EF=6m,计算DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
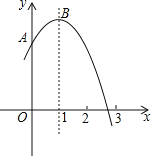
【题目】如图,抛物线![]() (m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线
(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.①抛物线![]() 与直线
与直线![]() 有且只有一个交点;②若点
有且只有一个交点;②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为
;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为![]() ;④点A关于直线
;④点A关于直线![]() 的对称点为C,点D、E分别在x轴和y轴上,当
的对称点为C,点D、E分别在x轴和y轴上,当![]() 时,四边形BCDE周长的最小值为
时,四边形BCDE周长的最小值为![]() .其中正确判断的序号是__
.其中正确判断的序号是__
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点O在AC上,以O为圆心,OC为半径作⊙O,过点A作AD⊥BO交BO的延长线于点D.则下列结论中:①点A、B、C、D在同一个圆上;②∠ABC=2∠CAD;③若∠BOC=∠BAD,则AB与⊙O相切,正确的结论是( )
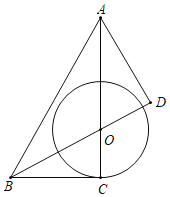
A.①②③B.①②C.②③D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为( )
,则k的值为( )
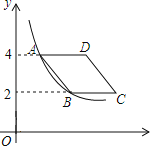
A. 2B. 3C. 4D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com