
【题目】如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
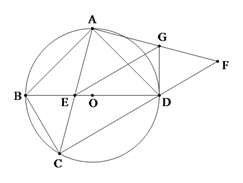
(1)证明:AC=AF;
(2)若AD=2,AF=![]() ,求AE的长;
,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
【答案】(1)证明见解析;
(2)AE的长为![]() ;
;
(3)证明见解析.
【解析】试题分析:(1)由圆的内接四边形的性质得:∠ABC+∠ADC=180°,又∠ADF+∠ADC=180°,故∠ABC=∠ADF,结合已知条件可证△ABC≌△ADF,从而可得结论;
(2)由(1)得AC=AF,由AB=AB得![]() ,得∠ADE=∠ACD.可证△ADE∽△ACD,得
,得∠ADE=∠ACD.可证△ADE∽△ACD,得![]() ,变换比例式从而得解;
,变换比例式从而得解;
(3)通过证明△ADG∽△AFD得∠ADG=∠F.再运用切线的判定定理即可得证.
试题解析:(1)证明:∵四边形ABCD内接于⊙O,∴∠ABC+∠ADC=180°.
∵∠ADF+∠ADC=180°,∴∠ABC=∠ADF.
在△ABC与△ADF中,
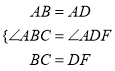 ,
,
∴△ABC≌△ADF.
∴AC=AF;
(2)由(1)得,AC=AF=![]() .
.
∵AB=AD,
∴![]()
∴∠ADE=∠ACD.
∵∠DAE=∠CAD,
∴△ADE∽△ACD.
∴![]() .
.
∴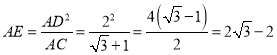 .
.
(3)证明:∵EG∥CF,∴ ![]() .
.
∴AG=AE.
由(2)得![]() ,∴
,∴![]() .
.
∵∠DAG=∠FAD,∴△ADG∽△AFD.
∴∠ADG=∠F.
∵AC=AF,∴∠ACD=∠F.
又∵∠ACD=∠ABD,
∴∠ADG=∠ABD.
∵BD为⊙O的直径,
∴∠BAD=90°.
∴∠ABD+∠BDA=90°.∴∠ADG+∠BDA=90°.
∴GD⊥BD.
∴DG为⊙O的切线.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】若将一副三角板按如图所示的方式放置,则下列结论不正确的是( ) 
A.∠1=∠3
B.如果∠2=30°,则有AC∥DE
C.如果∠2=30°,则有BC∥AD
D.如果∠2=30°,必有∠4=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4 , 给出如下结论: ①S1+S2=S3+S4;②S2+S4=S1+S3;③若S3=2S1 , 则S4=2S2;④若S1=S2 , 则P点在矩形的对角线上.
其中正确的结论的序号是(把所有正确结论的序号都填在横线上).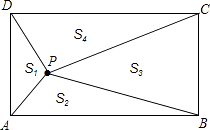
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1cm的若干个正方形叠加行成的图形,其中第一个图形由1个正方形组成,周长为4cm , 第二个图形由4个正方形组成,周长为10cm . 第三个图形由9个正方形组成,周长为16cm , 依次规律…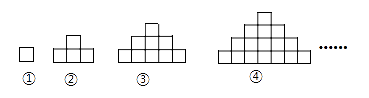
(1)第四个图形有个正方形组成,周长为cm .
(2)第n个图形有个正方形组成,周长为cm .
(3)若某图形的周长为58cm , 计算该图形由多少个正方形叠加形成.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com