
分析 ①利用描点法即可作出函数的图象;
②当y=0时,解方程求得x的值,当y>0时,就是函数图象在x轴上方的部分,据此即可解得;
③仿照上边的例子,首先作出函数y=x2-2x+1的图象,然后求得当y=4时对应的x的值,根据图象即可求解.
解答 解:①图所示: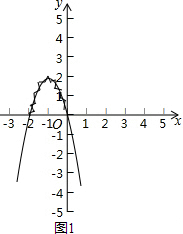 ;
;
②方程-2x2-4x=0即-2x(x+2)=0,
解得:x1=0,x2=-2;
则方程的解是x1=0,x2=-2,
图象如图1;
③函数y=x2-2x+1的图象是: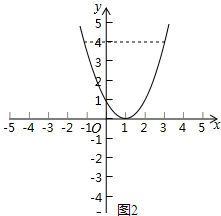
当y=4时,x2-2x+1=4,解得:x1=3,x2=-1.
则不等式的解集是:x≥3或x≤-1.
点评 本题考查了二次函数与不等式的关系,理解函数的图象在x轴上方,则函数值大于0是本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
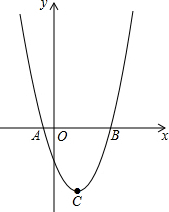 已知抛物线的顶点坐标C(4,-9),且过点(-1,16).
已知抛物线的顶点坐标C(4,-9),且过点(-1,16).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
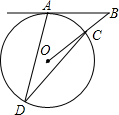 如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )
如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
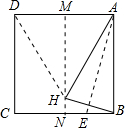 如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下得到△ADH,则下列选项正确的个数为( )
如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下得到△ADH,则下列选项正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com