
【题目】如图,![]() 是圆
是圆![]() 的直径,
的直径,![]() 是圆
是圆![]() 的切线,
的切线,![]() 交圆
交圆![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() .
.
(1)求证:![]()
(2)求证:![]() 四点共圆
四点共圆
(3)![]() 满足什么条件时,经过
满足什么条件时,经过![]() 的圆与
的圆与![]() 相切?并说明理由.
相切?并说明理由.
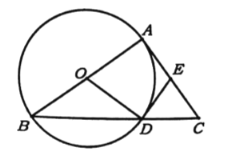
【答案】(1)见详解;(2)见详解;(3)等腰直角三角形.
【解析】
(1)连接AD,根据直径所对的圆周角是直角,可证得∠ADB=90°,再利用邻角互补的性质可得∠ADC=90°,再根据直角三角形斜边上的中线等于斜边的一半,可得AE=DE,由等边对等角可证得∠DAE=∠ADE,又由OA=OD,可得∠OAD=∠ODA,从而有∠OAD+∠DAE =∠ODA+∠ADE,再由切线的性质可得∠OAD+∠DAE =90°,从而结论得证;
(2)欲证四点共圆,只须证得四点到某一点的距离相等即可;
(3)由(1)可知AD⊥BC,所以要使经过![]() 的圆与
的圆与![]() 相切,则AD必为直径,由(2)可知OE必为直径,从而易证四边形OAED为正方形,从而有DE∥AB,且DE=
相切,则AD必为直径,由(2)可知OE必为直径,从而易证四边形OAED为正方形,从而有DE∥AB,且DE=![]() AB,所以D为BC的中点,而AD⊥BC,故可知
AB,所以D为BC的中点,而AD⊥BC,故可知![]() 为等腰直角三角形.
为等腰直角三角形.
(1) 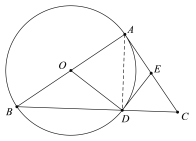
证明:如图所示,连接AD,
∵![]() 是圆
是圆![]() 的切线,
的切线,
∴∠BAE=90°
∴∠BAD+∠DAE=90°,
∵![]() 是圆
是圆![]() 的直径,
的直径,
∴∠ADB=∠ADC=90°.
∵点![]() 是
是![]() 的中点,
的中点,
∴AE=DE.
∴∠DAE=∠ADE,
∴∠BAD+∠ADE =90°.
∵OD=OA,
∴∠BAD=∠ODA.
∴∠ODA+∠ADE =90°.
即∠ODE=90°.
∴![]() .
.
(2) 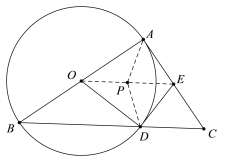
证明:如图所示,连接OE,取OE的中点P,连接PA,PD.
由(1)可知∠OAE=ODE=90°,
∵点P是OE的中点,
∴PA=PO=PE=PD,
∴![]() 四点共圆.
四点共圆.
(3) 当![]() 是等腰直角三角形时,经过
是等腰直角三角形时,经过![]() 的圆与
的圆与![]() 相切.
相切.
理由如下:如图所示:
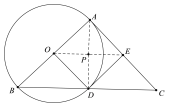
设⊙P为经过![]() 的圆.
的圆.
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴AB=AC,∠B=∠C=45°.
∵OB=OD,
∴∠B=∠ODB=45°.
∵O,E分别为AB,AC的中点,
∴OE∥BC.
∴∠POD=∠ODB=45°.
∵PO=PD,
∴∠PDO=∠POD=45°.
∴∠PDB=∠PDO+∠ODB =45°+45°=90°.
即PD⊥BC,
∴BC与圆P相切.
即当![]() 是等腰直角三角形时,经过
是等腰直角三角形时,经过![]() 的圆与
的圆与![]() 相切.
相切.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为![]() +2.其中正确结论的个数是
+2.其中正确结论的个数是
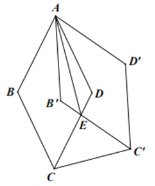
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研制出新产品,该产品的成本为每件2400元.在试销期间,购买不超过10件时,每件销售价为3000元;购买超过10件时,每多购买一件,所购产品的销售单价均降低5元,但最低销售单价为2600元。请解决下列问题:
(1)直接写出:购买这种产品 ________件时,销售单价恰好为2600元;
(2)设购买这种产品x件(其中x>10,且x为整数),该公司所获利润为y元,求y与x之间的函数表达式;
(3)该公司的销售人员发现:当购买产品的件数超过10件时,会出现随着数量的增多,公司所获利润反而减少这一情况.为使购买数量越多,公司所获利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BCD=90°,且BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)当α=125°时,∠ABC= °;
(2)求证:AC=CE;
(3)若△ABC的外心在其内部,直接写出α的取值范围.
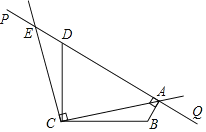
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在圆O中,弦AB⊥CD于E,弦AG⊥BC于F,CD与AG相交于点M.
(1)求证:弧BD=弧BG.
(2)如果AB=12,CM=4,求圆O的半径.
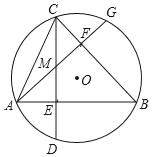
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为![]() ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | 1 |
根据图表提供的信息,解答下列问题:
(1)八年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有长度100米的围栏,要利用一面墙(墙长为25米)建羊圈,BC的长度不大于墙长。
⑴可以围成总面积为400平方米的三个大小相同的矩形羊圈?如果能,求羊圈的边长AB,BC各为多少米?如果不能,请说明理由。
⑵可以围成总面积为640平方米的三个大小相同的矩形羊圈?如果能,求羊圈的边长AB,BC各为多少米?如果不能,请说明理由。
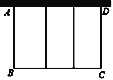
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com