
【题目】如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为![]() +2.其中正确结论的个数是
+2.其中正确结论的个数是
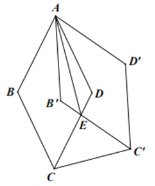
A.1B.2C.3D.4
【答案】B
【解析】
连结对角线![]() ,
,![]() ,∴
,∴![]() ,根据菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,得到
,根据菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,得到![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
∴![]() ,
,![]() ,并根据已知和菱形的性质可得:
,并根据已知和菱形的性质可得:![]() ∴
∴![]() ,
,![]() ,∴②不正确;
,∴②不正确;
可根据条件证明![]() ≌
≌![]() ,得到
,得到![]() ,并由
,并由![]() ,
,![]() 得到
得到![]() ≌
≌![]() ,∴①正确;∴
,∴①正确;∴![]() 为
为![]() 的角平分线,
的角平分线,
∴![]() (三线合一)∴③正确;根据
(三线合一)∴③正确;根据![]() ,求出
,求出![]() ,利用
,利用![]()
![]() ,∴
,∴![]()
∴![]() ,
, ![]()
∴四边形AB′ED的周长为:![]()
![]() ∴④不正确
∴④不正确
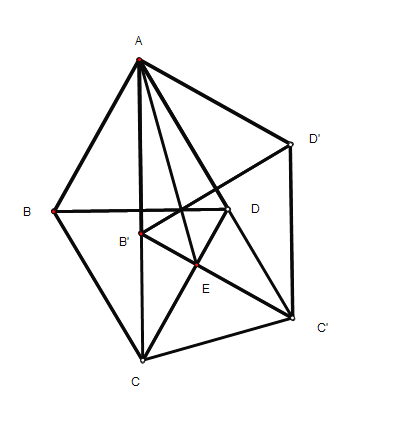
解:连结对角线![]() ,
,![]() ,∴
,∴![]() ,
,
∵菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,
∴![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
∴![]()
∴![]()
由题目已知和菱形的性质可得:![]()
∴![]()
∴![]()
∴![]() ,②不正确;
,②不正确;
在![]() 和
和![]() 中
中
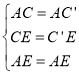
∴![]() ≌
≌![]()
∴![]()
∴由![]() ,
,![]()
∴![]() ≌
≌![]()
∴①正确;
∴![]() 为
为![]() 的角平分线,
的角平分线,
∴![]() (三线合一)
(三线合一)
∴③正确;
∵![]() ,
,
∴![]()
在菱形ABCD中,![]()
![]()
∴![]()
∴在![]() 中,
中,
![]() ,
, ![]()
∴四边形AB′ED的周长为:![]()
![]()
![]()
![]()
∴④不正确
综上所述,正确的有①③,
故选:B


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】(问题原型)如图,在![]() 中,对角线
中,对角线![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形.
是菱形.

(小海的证法)证明:
![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]() ,(第一步)
,(第一步)
![]() ,(第二步)
,(第二步)
![]() .(第三步)
.(第三步)
![]() 四边形
四边形![]() 是平行四边形.(第四步)
是平行四边形.(第四步)
![]() 四边形
四边形![]() 是菱形. (第五步)
是菱形. (第五步)
(老师评析)小海利用对角线互相平分证明了四边形![]() 是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
(挑错改错)(1)小海的证明过程在第________步上开始出现了错误.
(2)请你根据小海的证题思路写出此题的正确解答过程,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】胜利中学为丰富同学们的校园生活,举行“校园电视台主待人”选拔赛,现将36名参赛选手的成绩(单位:分)统计并绘制成频数分布直方图和扇形统计图,部分信息如下:
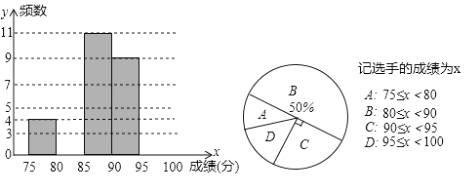
请根据统计图的信息,解答下列问题:
(1)补全频数分布直方图,并求扇形统计图中扇形![]() 对应的圆心角度数;
对应的圆心角度数;
(2)成绩在![]() 区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.
区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,过点
轴对称,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
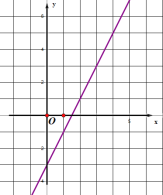
(1)求点![]() 的坐标;
的坐标;
(2)如果抛物线![]() 与线段
与线段![]() 有唯一公共点,
有唯一公共点,
①求抛物线![]() 的对称轴,
的对称轴,
②求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
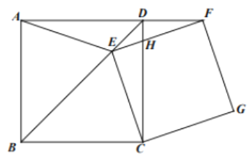
【题目】如图,在正方形ABCD中,E为对角线BD上的一点,点F在AD的延长线上,且∠CEF=90°,EF交CD于H,分别过点F,点C作EC和EF的平行线,交于点G.
(1)证明:AE=CE;
(2)证明:四边形ECGF是正方形;
(3)若正方形ABCD的边长为![]() ,且BE=BC,求此时ΔEDF的面积.
,且BE=BC,求此时ΔEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
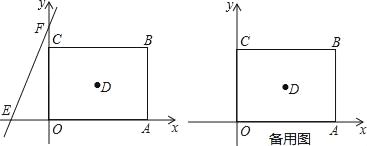
【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足﹣(a﹣4)2≥0,c=![]() +8.
+8.
(1)求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;
(2)直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为P(2,9),与x轴交于点A,B,与y轴交于点C(0,5).
(Ⅰ)求二次函数的解析式及点A,B的坐标;
(Ⅱ)设点Q在第一象限的抛物线上,若其关于原点的对称点Q′也在抛物线上,求点Q的坐标;
(Ⅲ)若点M在抛物线上,点N在抛物线的对称轴上,使得以A,C,M,N为顶点的四边形是平行四边形,且AC为其一边,求点M,N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
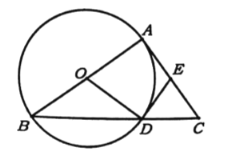
【题目】如图,![]() 是圆
是圆![]() 的直径,
的直径,![]() 是圆
是圆![]() 的切线,
的切线,![]() 交圆
交圆![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() .
.
(1)求证:![]()
(2)求证:![]() 四点共圆
四点共圆
(3)![]() 满足什么条件时,经过
满足什么条件时,经过![]() 的圆与
的圆与![]() 相切?并说明理由.
相切?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com