
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,过点
轴对称,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
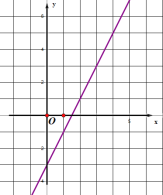
(1)求点![]() 的坐标;
的坐标;
(2)如果抛物线![]() 与线段
与线段![]() 有唯一公共点,
有唯一公共点,
①求抛物线![]() 的对称轴,
的对称轴,
②求![]() 的取值范围.
的取值范围.
【答案】(1)(3,3);(2)①见解析;②见解析.
【解析】
(1)根据题意分别求出点A、B、C的坐标;
(2)①将抛物线![]() 化成顶点式,即可得抛物线的对称轴,顶点的坐标;
化成顶点式,即可得抛物线的对称轴,顶点的坐标;
②分类讨论当n>3时;当n=3时;当0<n<3时,抛物线y=nx2-4nx+5n(n>0)与线段BC有唯一公共点,求n的取值范围.
解:(1)∵直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
∴点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,
,![]() 为直线
为直线![]() .
.
∵直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)①∵抛物线![]() ,
,
∴![]() .
.
∴抛物线的顶点坐标为![]() ,对称轴为直线
,对称轴为直线![]() .
.
②∵点![]() ,点
,点![]() ,
,
当![]() 时,抛物线最小值为
时,抛物线最小值为![]() ,与线段
,与线段![]() 无公共点;
无公共点;
当![]() 时,抛物线顶点为
时,抛物线顶点为![]() ,在线段
,在线段![]() 上.
上.
此时抛物线与线段![]() 有一个公共点;
有一个公共点;
当![]() 时,抛物线最小值为
时,抛物线最小值为![]() ,与直线
,与直线![]() 有两个交点.
有两个交点.
如果抛物线![]() 经过点
经过点![]() ,则
,则![]() ,解得
,解得![]() .
.
由抛物线的对称轴为直线![]() ,可知抛物线经过点
,可知抛物线经过点![]() .
.
点![]() 不在线段
不在线段![]() 上,此时抛物线与线段
上,此时抛物线与线段![]() 有一个公共点
有一个公共点![]() .
.
如果抛物线![]() 经过点
经过点![]() ,则
,则![]() ,解得
,解得![]() .
.
由抛物线的对称轴为直线![]() ,可知抛物线经过点
,可知抛物线经过点![]() .
.
点![]() 在线段
在线段![]() 上,此时抛物线与线段
上,此时抛物线与线段![]() 有两个公共点.
有两个公共点.
综上所述,当![]() 或
或![]() 时,抛物线与线段
时,抛物线与线段![]() 有一个公共点.
有一个公共点.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
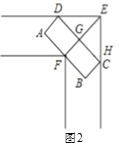
【题目】车辆转弯时,能否顺利通过直角弯道的标准是:车辆是否可以行使到和路的边界夹角是45°的位置(如图1中②的位置),例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,则车辆就能通过.
(1)试说明长8m,宽3m的消防车不能通过该直角转弯;
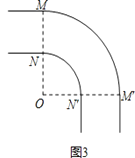
(2)为了能使长8m,宽3m的消防车通过该弯道,可以将转弯处改为圆弧(分别是以O为圆心,以OM和ON为半径的弧),具体方案如图3,其中OM⊥OM′,请你求出ON的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
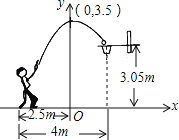
【题目】一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A. 此抛物线的解析式是y=﹣![]() x2+3.5
x2+3.5
B. 篮圈中心的坐标是(4,3.05)
C. 此抛物线的顶点坐标是(3.5,0)
D. 篮球出手时离地面的高度是2m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,经过点
,经过点![]() .
.
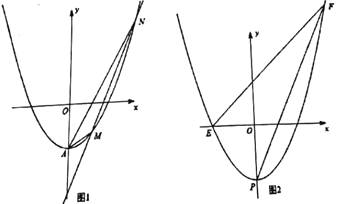
(1)求抛物线![]() 的解析式;
的解析式;
(2)如图1,直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() 的值;
的值;
(3)如图2,将抛物线![]() 向下平移
向下平移![]() 个单位长度得到抛物线
个单位长度得到抛物线![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() ,交
,交![]() 轴的负半轴于点
轴的负半轴于点![]() ,点
,点![]() 在抛物线
在抛物线![]() 上.
上.
①求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
②若![]() ,求
,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为![]() +2.其中正确结论的个数是
+2.其中正确结论的个数是
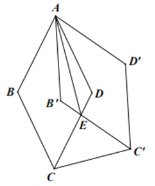
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作 EF∥AD,与AC、DC 分别交于点G,F,H为CG的中点,连结DE、 EH、DH、FH.下列结论:①EG=DF;②△EHF≌△DHC;③∠AEH+∠ADH=180°;④若![]() ,则
,则![]() .其中结论正确的有( )
.其中结论正确的有( )
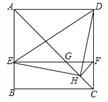
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2, 0),则点C的坐标为( )
经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2, 0),则点C的坐标为( )
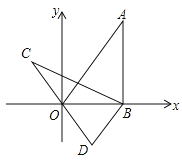
A.(﹣1,![]() )B.(﹣2,
)B.(﹣2,![]() )C.(
)C.(![]() ,1)D.(
,1)D.(![]() ,2)
,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
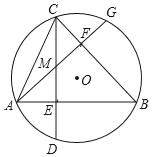
【题目】如图,在圆O中,弦AB⊥CD于E,弦AG⊥BC于F,CD与AG相交于点M.
(1)求证:弧BD=弧BG.
(2)如果AB=12,CM=4,求圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com