
【题目】已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,经过点
,经过点![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
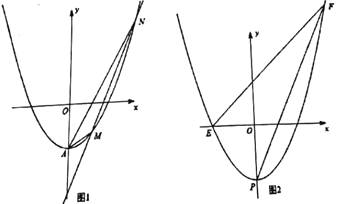
(2)如图1,直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,若
两点,若![]() ,求
,求![]() 的值;
的值;
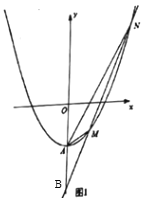
(3)如图2,将抛物线![]() 向下平移
向下平移![]() 个单位长度得到抛物线
个单位长度得到抛物线![]() ,抛物线
,抛物线![]() 的顶点为
的顶点为![]() ,交
,交![]() 轴的负半轴于点
轴的负半轴于点![]() ,点
,点![]() 在抛物线
在抛物线![]() 上.
上.
①求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
②若![]() ,求
,求![]() ,
,![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①点
;(3)①点![]() 的坐标为
的坐标为![]() ;②
;②![]() .
.
【解析】
(1)根据顶点坐标设解析式为y=ax2-2,把B点坐标代入可求出a的值,即可得答案;(2)设直线![]() 交
交![]() 轴点
轴点![]() ,可得B的坐标为(0,4),可得AB的长,根据
,可得B的坐标为(0,4),可得AB的长,根据![]() 可得
可得![]() ,联立二次函数和一次函数的解析式可得
,联立二次函数和一次函数的解析式可得![]() ,根据一元二次方程根与系数的关系可得
,根据一元二次方程根与系数的关系可得![]() ,
,![]() ,进而可得答案;(3)①根据平移的性质可得抛物线C1的解析式,根据当F在抛物线C1上,可得
,进而可得答案;(3)①根据平移的性质可得抛物线C1的解析式,根据当F在抛物线C1上,可得![]() ,可得点P的坐标,令y=0,即可求出E点坐标;②作
,可得点P的坐标,令y=0,即可求出E点坐标;②作![]() 轴于点
轴于点![]() ,根据E、F坐标可得EH=FH,可得
,根据E、F坐标可得EH=FH,可得![]() ,根据∠FEO=2∠EFP及平行线的性质可得∠FPO=∠EFP =22.5°,设
,根据∠FEO=2∠EFP及平行线的性质可得∠FPO=∠EFP =22.5°,设![]() 交
交![]() 轴于点
轴于点![]() ,可得PD=DF=
,可得PD=DF=![]() OH,根据等腰直角三角形的性质可用a表示出PD的长,OH=a,列方程求出可得a的值,把a代入
OH,根据等腰直角三角形的性质可用a表示出PD的长,OH=a,列方程求出可得a的值,把a代入![]() 即可求出m的值.
即可求出m的值.
(1)已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,
,
∴设抛物线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得:6=16a-2,
代入得:6=16a-2,
解得:![]() ,
,
∴抛物线![]() 的解析式为
的解析式为![]() .
.
(2)设直线![]() 交
交![]() 轴点
轴点![]() ,则点
,则点![]() 的坐标
的坐标![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
由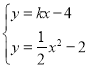 得
得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(3)①依题意得抛物线![]() 的解析式为
的解析式为![]() .
.
点![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,
,
∴顶点![]() 的坐标为
的坐标为![]() ,
,
令![]() ,即
,即![]() .
.
∴![]() ,
,![]() (舍去),
(舍去),
∴点![]() 的坐标为
的坐标为![]() .
.
②作![]() 轴于点
轴于点![]() ,
,
∵E(2-a,0),F(a,2a-2),
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∵FH//y轴,
∴∠FPO=∠PFH=22.5°,
∴∠FPO=∠EFP,
∴PD=FD,
设![]() 交
交![]() 轴于点
轴于点![]() ,过D作DG⊥FH于G,则DG=OH,
,过D作DG⊥FH于G,则DG=OH,
∵∠EFH=45°,
∴![]() ,
,
∵∠FEH=45°,a>2,
∴OD=OE=a-2,
∴PD=a-2-![]() =
=![]() ,
,
∵HO=a,
∴![]() ,
,
∴![]() ,
,![]() (舍去),
(舍去),
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加x元.求:
(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)该宾馆每天的房间收费z(元)关于x(元)的函数关系式;
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD 是△ABC 的角平分线,DE,DF 分别是△BAD 和△ACD 的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形 AEDF 是正方形;④AE+DF=AF+DE.其中正确的是_________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,过点
轴对称,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
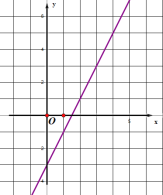
(1)求点![]() 的坐标;
的坐标;
(2)如果抛物线![]() 与线段
与线段![]() 有唯一公共点,
有唯一公共点,
①求抛物线![]() 的对称轴,
的对称轴,
②求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进了一批单价为100元的名牌衬衫,当销售价为150元时,平均每天可售出20件,为了扩大销售、增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果衬衫单价每降价1元,商场平均每天可多售出4件,另外,这批衬衫平均每天要扣除其它成本50元,若商场平均每天盈利2 750元,衬衫单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O 的内接△ABC 中,∠ABC=30°,AC 的延长线与过点 B 的⊙O 的切线相交于点 D,若⊙O 的半径 OC=1,BD∥OC,则 CD 的长为( )
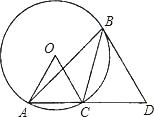
A. 1+![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com