
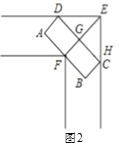
【题目】车辆转弯时,能否顺利通过直角弯道的标准是:车辆是否可以行使到和路的边界夹角是45°的位置(如图1中②的位置),例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,则车辆就能通过.
(1)试说明长8m,宽3m的消防车不能通过该直角转弯;
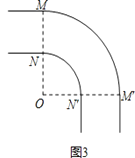
(2)为了能使长8m,宽3m的消防车通过该弯道,可以将转弯处改为圆弧(分别是以O为圆心,以OM和ON为半径的弧),具体方案如图3,其中OM⊥OM′,请你求出ON的最小值.

【答案】(1)消防车不能通过该直角转弯;(2)ON至少为4.5米.
【解析】
(1)过点F作FH⊥EC于点H,根据道路的宽度求出FH=EH=4m,然后根据等腰直角三角形的性质求出EF、GE的长度,相减即可得到GF的长度,如果不小于车身宽度,则消防车能通过,否则,不能通过;
(2)假设车身C、D分别与点M′、M重合,根据等腰直角三角形的性质求出OG=![]() CD=4,OC=
CD=4,OC=![]() CG=4
CG=4![]() ,然后求出OF的长度,从而求出可以通过的车宽FG的长度,如果不小于车宽,则消防车能够通过,否则,不能通过;设ON=x,表示出OC=x+4,OG=x+3,又OG=
,然后求出OF的长度,从而求出可以通过的车宽FG的长度,如果不小于车宽,则消防车能够通过,否则,不能通过;设ON=x,表示出OC=x+4,OG=x+3,又OG=![]() CD=4,在Rt△OCG中,利用勾股定理列式进行计算即可求出ON的最小值.
CD=4,在Rt△OCG中,利用勾股定理列式进行计算即可求出ON的最小值.
解:(1)消防车不能通过该直角转弯.
理由如下:如图,作FH⊥EC,垂足为H,
∵FH=EH=4,
∴EF=4![]() ,且∠GEC=45°,
,且∠GEC=45°,
∵GC=4,
∴GE=GC=4,
∴GF=4![]() ﹣4<3,
﹣4<3,
即GF的长度未达到车身宽度,
∴消防车不能通过该直角转弯.
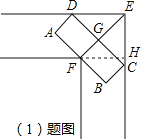
(2)若C、D分别与M′、M重合,则△OGM为等腰直角三角形,
∴OG=4,OM=4![]() ,
,
∴OF=ON=OM﹣MN=4![]() ﹣4,
﹣4,
∴FG=OG﹣OF=![]() ×8﹣(4
×8﹣(4![]() ﹣4)=8﹣4
﹣4)=8﹣4![]() <3,
<3,
∴C、D在![]() 上,
上,
设ON=x,连接OC,在Rt△OCG中,
OG=x+3,OC=x+4,CG=4,
由勾股定理得,OG2+CG2=OC2,
即(x+3)2+42=(x+4)2,
解得x=4.5.
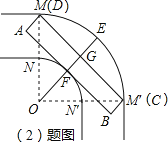
答:ON至少为4.5米.


科目:初中数学 来源: 题型:
【题目】如图(1),![]() 为等腰三角形,
为等腰三角形,![]() ,
,![]() 点是底边
点是底边![]() 上的一个动点,
上的一个动点,![]() ,
,![]() .
.
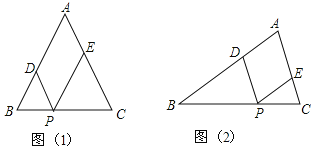
(1)用![]() 表示四边形
表示四边形![]() 的周长为 ;
的周长为 ;
(2)点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形,请说明理由;
是菱形,请说明理由;
(3)如果![]() 不是等腰三角形图(2),其他条件不变,点
不是等腰三角形图(2),其他条件不变,点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形(不必说明理由).
是菱形(不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 |
|
|
|
|
|
类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 11 | 20 | 40 |
| 4 |
请你根据以上信息,回答下列问题:
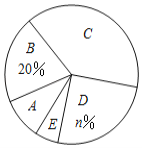
(1)统计表中![]() 的值为_______,统计图中
的值为_______,统计图中![]() 的值为______,
的值为______,![]() 类对应扇形的圆心角为_____度;
类对应扇形的圆心角为_____度;
(2)该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;
(3)样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是指空气中直径小于或等于
是指空气中直径小于或等于![]() 的颗粒物,它对人体健康和大气环境造成不良影响,下表是根据《全国城市空气质量报告》中的部分数据制作的统计表.根据统计表回答下列问题,
的颗粒物,它对人体健康和大气环境造成不良影响,下表是根据《全国城市空气质量报告》中的部分数据制作的统计表.根据统计表回答下列问题,

(1)2018年7~12月![]() 平均浓度的中位数为
平均浓度的中位数为 ![]() ;
;
(2)“扇形统计图”和“折线统计图”中,更能直观地反映2018年7~12月![]() 平均浓度变化过程和趋势的统计图是 ;
平均浓度变化过程和趋势的统计图是 ;
(3)某同学观察统计表后说:“2018年7~12月与2017年同期相比,空气质量有所改善”,请你用一句话说明该同学得出这个结论的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题原型)如图,在![]() 中,对角线
中,对角线![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形.
是菱形.

(小海的证法)证明:
![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]() ,(第一步)
,(第一步)
![]() ,(第二步)
,(第二步)
![]() .(第三步)
.(第三步)
![]() 四边形
四边形![]() 是平行四边形.(第四步)
是平行四边形.(第四步)
![]() 四边形
四边形![]() 是菱形. (第五步)
是菱形. (第五步)
(老师评析)小海利用对角线互相平分证明了四边形![]() 是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
(挑错改错)(1)小海的证明过程在第________步上开始出现了错误.
(2)请你根据小海的证题思路写出此题的正确解答过程,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,过点
轴对称,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
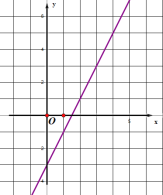
(1)求点![]() 的坐标;
的坐标;
(2)如果抛物线![]() 与线段
与线段![]() 有唯一公共点,
有唯一公共点,
①求抛物线![]() 的对称轴,
的对称轴,
②求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com