
分析 (1)把所求的式子化成(x-y)2-xy的形式,然后代入求解求解;
(2)把所求的式子化成 $\frac{{x}^{2}+{y}^{2}-4xy}{xy}$=$\frac{(x-y)^{2}-2xy}{xy}$=$\frac{(x-y)^{2}}{xy}$-2形式,然后代入求解求解.
解答 解:(1)原式=(x-y)2-xy
知x=3+2$\sqrt{2}$,y=3-2$\sqrt{2}$,则x=3+2$\sqrt{2}$,y=3-2$\sqrt{2}$时,原式=(4$\sqrt{2}$)2-(3+2$\sqrt{2}$)(3-2$\sqrt{2}$)=32-(9-8)=32-1=31;
(2)原式=$\frac{{x}^{2}+{y}^{2}-4xy}{xy}$=$\frac{(x-y)^{2}-2xy}{xy}$=$\frac{(x-y)^{2}}{xy}$-2,
当x=3+2$\sqrt{2}$,y=3-2$\sqrt{2}$时,原式=$\frac{(4\sqrt{2})^{2}}{(3+2\sqrt{2})(3-2\sqrt{2})}$-2=$\frac{32}{9-8}$-2=32-2=30.
点评 本题考查了二次根式的化简求值,正确理解平方差公式的结构,正确对所求的式子进行变形是关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y1>y2 | D. | y2>y1>y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC,按要求完成下列各题:
如图,△ABC,按要求完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -52=(-5)×(-5) | B. | 32=3×2 | C. | 32=3+3 | D. | -(-$\frac{1}{2}$)2=-$\frac{1}{2}$×$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
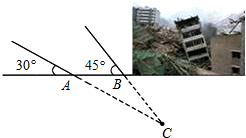 一方有难八方支援.安徽地震局救援队在某次地震救援中,探测出某建筑物废墟下方点C处有生命迹象,在废墟一侧某面上选两探测点A、B,AB相距2.1米,探测线与地面的夹角分别是35°和45°(如图),试确定生命所在点C与探测面的距离(参考数据$\sqrt{2}$≈1.4,≈1.7)
一方有难八方支援.安徽地震局救援队在某次地震救援中,探测出某建筑物废墟下方点C处有生命迹象,在废墟一侧某面上选两探测点A、B,AB相距2.1米,探测线与地面的夹角分别是35°和45°(如图),试确定生命所在点C与探测面的距离(参考数据$\sqrt{2}$≈1.4,≈1.7)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com