
【题目】如图,在直角坐标系中,抛物线![]() 与y轴交于点D(0,3).
与y轴交于点D(0,3).
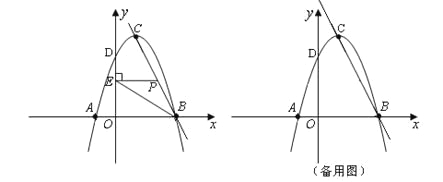
(1)直接写出c的值;
(2)若抛物线与x轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
(3)已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥y轴,垂足为E,连结BE.设点P的坐标为(x,y),△PBE的面积为s,求s与x的函数关系式,写出自变量x的取值范围,并求出s的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为r的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求r的值,并直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)c=3;(2)![]() ;(3)①S=-x2+3x=-(x-
;(3)①S=-x2+3x=-(x-![]() )2+
)2+![]() (1<x<3);当x=
(1<x<3);当x=![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() ;②存在点P1(
;②存在点P1(![]() ),或P2(
),或P2(![]() ),此时r1=
),此时r1=![]() ;点P3(
;点P3(![]() ),或P4(
),或P4(![]() ),此时r2=
),此时r2=![]() ,理由见解析.
,理由见解析.
【解析】
(1)将点D(0,3)直接代入解析式即可;
(2)先求出顶点C坐标为(1,4),以及与x轴的交点坐标,即令y=0时,得到点B(3,0)代入一次函数解析式即可求得答案;
(3)根据S=![]() PE·OE,利用P点在线段BC上,可表示出PE,OE,得到S=
PE·OE,利用P点在线段BC上,可表示出PE,OE,得到S=![]() ,变形为顶点式后求出最大值即可.第②小问,根据两圆内切与外切进行分类讨论,分别用r表示出CQ,PQ,CP的长度,再利用勾股定理即可求出r长度和P点坐标.
,变形为顶点式后求出最大值即可.第②小问,根据两圆内切与外切进行分类讨论,分别用r表示出CQ,PQ,CP的长度,再利用勾股定理即可求出r长度和P点坐标.
解:(1)∵将D(0,3)代入解析式
∴c=3
(2)由(1)知抛物线为:
y=-x2+2x+3,配方得y=-(x-1)2+4
∴顶点C坐标为(1,4)
令y=0,得x1=-1,x2=3
∴ B(3,0)
设直线BC解析式为:![]() (
(![]() ),把B、C两点坐标代入,
),把B、C两点坐标代入,
得![]() 解得
解得![]() .
.
∴直线BC解析式为![]()
(3)①∵点P(x,y)在![]() 的图象上,
的图象上,
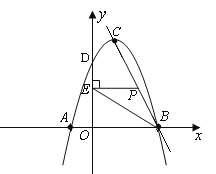
∴PE=x,OE=-2x+6
∴s=![]() PE·OE=
PE·OE=![]()
∴![]()
![]() .
.
∵x=![]() 符合1<x<3,
符合1<x<3,
∴当x=![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() .
.
②答:存在.
如图,设抛物线的对称轴交x轴于点F,则CF=4,BF=2
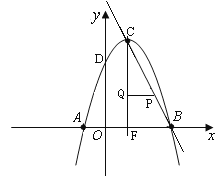
过P作PQ⊥CF于Q,则Rt△CPQ∽Rt△CBF
∴![]() ,即
,即![]()
∴CQ=2r
当⊙P与⊙C外切时,CP=r+1
∵CQ2+PQ2=CP2
∴(2r)2+r2=(r+1)2
解得r=![]() (r=
(r=![]() 舍去)
舍去)
此时P1(![]() ),或P2(
),或P2(![]() )
)
当⊙P与⊙C内切时,CP=r-1.
∵CQ2+PQ2=CP2
∴(2r)2+r2=(r-1)2
解得r=![]() (r=
(r= ![]() 舍去)
舍去)
此时P3(![]() ),或P4(
),或P4(![]() ).
).
∴当r1=![]() , r2=
, r2=![]() 时,⊙P与⊙C相切.
时,⊙P与⊙C相切.
点P的坐标为P1(![]() ),或P2(
),或P2(![]() ),
),
P3(![]() ),或P4(
),或P4(![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过定点
经过定点![]() 、
、![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.
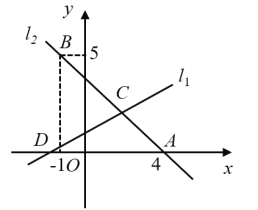
(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 的周长最短?若存在,请求出点
的周长最短?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
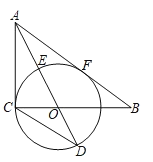
【题目】如图,在Rt△ABC中,∠ACB=90°,O是线段BC上一点,以O为圆心,OC为半径作⊙O,AB与⊙O相切于点F,直线AO交⊙O于点E,D.
(1)求证:AO是△CAB的角平分线;
(2)若tan∠D=![]() ,AE=2,求AC的长.
,AE=2,求AC的长.
(3)在(2)条件下,连接CF交AD于点G,⊙O的半径为3,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
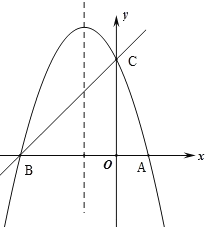
【题目】如图,已知抛物线![]() (a≠0)的对称轴为直线
(a≠0)的对称轴为直线![]() ,且抛物线经过A(1,0),C(0,3)两点,与
,且抛物线经过A(1,0),C(0,3)两点,与![]() 轴交于点B.
轴交于点B.
(1)若直线![]() 经过B,C两点,求直线BC和抛物线的解析式;
经过B,C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点M,使MA+MC的值最小,求点M的坐标;
上找一点M,使MA+MC的值最小,求点M的坐标;
(3)设P为抛物线的对称轴![]() 上的一个动点,求使ΔBPC为直角三角形的点P的坐标.
上的一个动点,求使ΔBPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
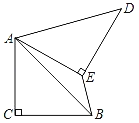
【题目】如图,梯形ABCD中,AD∥BC,BA=AD=DC,点E在CB延长线上,BE=AD,连接AC、AE.

⑴ 求证:AE=AC;
⑵ 若AB⊥AC, F是BC的中点,试判断四边形AFCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励下岗工人再就业,某地市政府规定,企业按成本价提供产品给下岗人员自主销售,成本价与出厂价之间的差价由政府承担.老李按照政策投资销售本市生产的一种儿童面条.已知这种儿童面条的成本价为每袋12元,出厂价为每袋16元,每天销售量![]() (袋)与销售单价
(袋)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)老李在开始创业的第1天将销售单价定为17元,那么政府这一天为他承担的总差价为多少元?
(2)设老李获得的利润为![]() (元),当销售单价为多少元时,每天可获得最大利润?
(元),当销售单价为多少元时,每天可获得最大利润?
(3)物价部门规定,这种面条的销售单价不得高于24元,如果老李想要每天获得的利润不低于216元,那么政府每天为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则∠BED的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com