
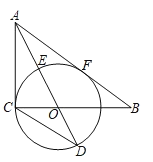
【题目】如图,在Rt△ABC中,∠ACB=90°,O是线段BC上一点,以O为圆心,OC为半径作⊙O,AB与⊙O相切于点F,直线AO交⊙O于点E,D.
(1)求证:AO是△CAB的角平分线;
(2)若tan∠D=![]() ,AE=2,求AC的长.
,AE=2,求AC的长.
(3)在(2)条件下,连接CF交AD于点G,⊙O的半径为3,求CF的长.
【答案】(1)证明见解析;(2)4;(3)![]() .
.
【解析】
(1)连接OF,可得OF⊥AB,由∠ACB=90°,OC=OF,可得出结论;
(2)连接CE,先求证∠ACE=∠ODC,然后可知△ACE∽△ADC,所以![]() ,结合tan∠D=
,结合tan∠D=![]() =
=![]() ,即可得到结论;
,即可得到结论;
(3)连接CF交AD于点M,由(2)可知,AC2=AEAD,先求出AE,AC的长,则AO可求出,证△CMO∽△ACO,可得OC2=OMOA,求出OM,CM,结合CF=2CM,即可求解.
(1)证明:连接OF.
∵AB与⊙O相切于点F,∴OF⊥AB.
∵∠ACB=90°,OC=OF,∴∠OAF=∠OAC,
即AO是△ABC的角平分线;
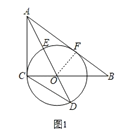
(2)如图2,连接CE,
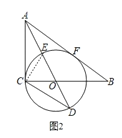
∵ED是⊙O的直径,∴∠ECD=90°,∴∠ECO+∠OCD=90°.
∵∠ACB=90°,∴∠ACE+∠ECO=90°,∴∠ACE=∠OCD.
∵OC=OD,∴∠OCD=∠ODC,∴∠ACE=∠ODC.
∵∠CAE=∠CAE,∴△ACE∽△ADC,∴![]() .
.
∵tan∠D=![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ;∵AE=2∴AC=4
;∵AE=2∴AC=4
(3)由(2)可知:AE=2,AC=4,∴AO=AE+OE=2+3=5,
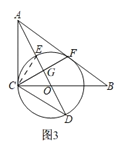
如图3,连接CF交AD于点G.
∵AC,AF是⊙O的切线,∴AC=AF,∠CAO=∠OAF,∴CF⊥AO,∴∠ACO=∠CGO=90°.
∵∠COG=∠AOC,∴△CGO∽△ACO,∴![]() ,∴OC2=OGOA,∴OG=
,∴OC2=OGOA,∴OG=![]() ,∴CG=
,∴CG=![]() =
=![]() ,∴CF=2CG=
,∴CF=2CG=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,点O是正方形ABCD两对角线的交点. 分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转![]() 角(0°<
角(0°< ![]() <360°)得到正方形
<360°)得到正方形![]() ,如图2.
,如图2.
①在旋转过程中,当∠![]() 是直角时,求
是直角时,求![]() 的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)
的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)
②若正方形ABCD的边长为1,在旋转过程中,求![]() 长的最大值和此时
长的最大值和此时![]() 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由.
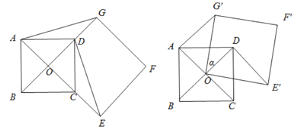
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;(2)若AB=14,DE=8,求sin∠AEB的值.
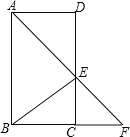
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,![]() .,已知点A,B的横坐标分别为1、2,△OAC与△ABD的面积之和为3,则k的值为( )
.,已知点A,B的横坐标分别为1、2,△OAC与△ABD的面积之和为3,则k的值为( )
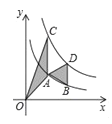
A.5B.4C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,∠C=90°,若AC=6,BC=8,AD平分∠CAB交CB于D.
(1)求CD的长;
(2)如图2,E是AC上一点,连ED,过D作DE的垂线交AB于F,若ED=DF,求CE的长;
(3)如图3,在(2)条件下,点P在FD延长线上,过F作ED的平行线QF,连PE、PQ,若∠QPF=2∠PED=2α,PQ=5PD,(QF>PF),求QF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线![]() 与y轴交于点D(0,3).
与y轴交于点D(0,3).
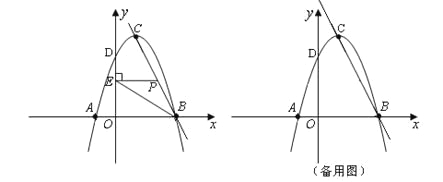
(1)直接写出c的值;
(2)若抛物线与x轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
(3)已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥y轴,垂足为E,连结BE.设点P的坐标为(x,y),△PBE的面积为s,求s与x的函数关系式,写出自变量x的取值范围,并求出s的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为r的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求r的值,并直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为m;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为n.
(1)用列表法或画树状图表示出(m,n)的所有可能出现的结果;
(2)小明认为点(m,n)在一次函数y=x+2的图象上的概率一定大于在反比例函数y=![]() 的图象上的概率,而小华却认为两者的概率相同.你赞成谁的观点?分别求出点(m,n)在两个函数图象上的概率,并说明谁的观点正确.
的图象上的概率,而小华却认为两者的概率相同.你赞成谁的观点?分别求出点(m,n)在两个函数图象上的概率,并说明谁的观点正确.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com