练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】设x1、x2是关于x的方程2x2﹣4mx+2m2+3m+2＝0的两个实根，当m＝_____时，x12+x22有最小值为_____．

    【答案】- ；

    【解析】

    由根与系数的关系知x12+x22是关于m的二次函数，是否是在抛物线的顶点处取得最小值，就要看自变量m的取值范围，从判别式入即可求解．

    解：∵x1、x2是方程2x2﹣4mx+2m2+3m+2＝0的两个实根，

    ∴△＝（﹣4m）2﹣4×2×（2m2+3m+2）≥0，可得m≤﹣，

    又∵x1+x2＝2m，x1x2＝，

    ∴x12+x22＝（x1+x2）2﹣2x1x2＝（2m）2﹣2×＝2（m﹣）2﹣，

    ∵m≤﹣，

    ∴当m＝﹣时，x12+x22取得最小值为2×（﹣）2﹣＝．

    故答案为：﹣，．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

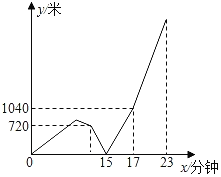
    【题目】小刚从家出发匀速步行去学校上学．几分钟后发现忘带数学作业，于是掉头原速返回并立即打电话给爸爸，挂断电话后爸爸立即匀速跑步去追小刚，同时小刚以原速的两倍匀速跑步回家，爸爸追上小刚后以原速的倍原路步行回家．由于时间关系小明拿到作业后同样以之前跑步的速度赶往学校，并在从家出发后23分钟到校（小刚被爸爸追上时交流时间忽略不计）．两人之间相距的路程y（米）与小刚从家出发到学校的步行时间x（分钟）之间的函数关系如图所示，则小刚家到学校的路程为_____米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

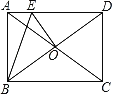
    【题目】如图，矩形ABCD的对角线AC与BD交于点O，点E在AD上，且DE＝CD，连接OE，∠ABE＝∠ACB，若AE＝2，则OE的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，为等边的高，，点P为直线上的动点（不与点B重合），连接，将线段绕点P逆时针旋转60°，得到线段，连接、．

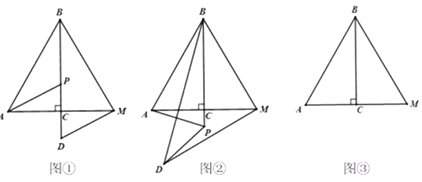
    （1）问题发现：如图①，当点D在直线上时，线段与的数量关系为_________，_________；

    （2）拓展探究：如图②，当点P在的延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；

    （3）问题解决：当时，请直接写出线段的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

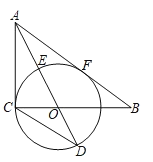
    【题目】如图，在Rt△ABC中，∠ACB=90°，O是线段BC上一点，以O为圆心，OC为半径作⊙O，AB与⊙O相切于点F，直线AO交⊙O于点E，D．

    （1）求证：AO是△CAB的角平分线；

    （2）若tan∠D=，AE=2，求AC的长．

    （3）在（2）条件下，连接CF交AD于点G，⊙O的半径为3，求CF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，点C是弧AB的中点，连接AC并延长至点D，使CD＝AC，点E是OB上一点，且，CE的延长线交D的延长线于点F，AF交⊙O于点H，连接BH．

    （1）求证：BD是⊙O的切线；

    （2）当OB＝2时，求AH的长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

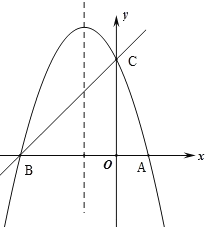
    【题目】如图，已知抛物线(a≠0)的对称轴为直线，且抛物线经过A(1，0)，C(0，3)两点，与轴交于点B．

    （1）若直线经过B，C两点，求直线BC和抛物线的解析式；

    （2）在抛物线的对称轴上找一点M，使MA+MC的值最小，求点M的坐标；

    （3）设P为抛物线的对称轴上的一个动点，求使ΔBPC为直角三角形的点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为鼓励下岗工人再就业，某地市政府规定，企业按成本价提供产品给下岗人员自主销售，成本价与出厂价之间的差价由政府承担．老李按照政策投资销售本市生产的一种儿童面条．已知这种儿童面条的成本价为每袋12元，出厂价为每袋16元，每天销售量（袋）与销售单价（元）之间的关系近似满足一次函数：．

    （1）老李在开始创业的第1天将销售单价定为17元，那么政府这一天为他承担的总差价为多少元？

    （2）设老李获得的利润为（元），当销售单价为多少元时，每天可获得最大利润？

    （3）物价部门规定，这种面条的销售单价不得高于24元，如果老李想要每天获得的利润不低于216元，那么政府每天为他承担的总差价最少为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设都是实数，且．我们规定：满足不等式的实数的所有值的全体叫做闭区间、表示为．对于一个函数，如果它的自变量与函数值满足：当时，有，我们就称此函数是闭区间上的“闭函数”．

    （1）反比例函数是闭区间上的“闭函数”吗？请判断并说明理由；

    （2）若一次函数是闭区间上的“闭函数”，求此一次函数的解析式；

    （3）若实数满足.且，当二次函数是闭区间上的“闭函数”时，求的值．

    查看答案和解析>>

    同步练习册答案