
【题目】如图,![]() 为等边
为等边![]() 的高,
的高,![]() ,点P为直线
,点P为直线![]() 上的动点(不与点B重合),连接
上的动点(不与点B重合),连接![]() ,将线段
,将线段![]() 绕点P逆时针旋转60°,得到线段
绕点P逆时针旋转60°,得到线段![]() ,连接
,连接![]() 、
、![]() .
.
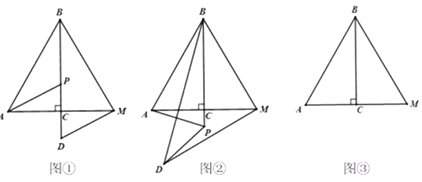
(1)问题发现:如图①,当点D在直线![]() 上时,线段
上时,线段![]() 与
与![]() 的数量关系为_________,
的数量关系为_________,![]() _________;
_________;
(2)拓展探究:如图②,当点P在![]() 的延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
的延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)问题解决:当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长度.
的长度.
【答案】(1)相等;90°;(2)成立,证明见解析;(3)4或![]()
【解析】
(1)连接AD,通过SAS证明![]() ,然后对应边、对应角相等、等量减等量,即可得出结论;
,然后对应边、对应角相等、等量减等量,即可得出结论;
(2)连接AD,通过SAS证明![]() ,然后对应边、对应角相等、等量加等量,即可得出结论;
,然后对应边、对应角相等、等量加等量,即可得出结论;
(3)通过前两问,我们知道![]() 是等边三角形,点D的轨迹是AP旋转60°得来的,A为定点,P再BC上运动是主动点,D为从动点,根据瓜豆原理可以得出D的轨迹是一条直线;BM长为定值、
是等边三角形,点D的轨迹是AP旋转60°得来的,A为定点,P再BC上运动是主动点,D为从动点,根据瓜豆原理可以得出D的轨迹是一条直线;BM长为定值、![]() 也为定值,利用定弦定角模型可知点D还应在圆弧上,因为点P可能在B点上方,还可能在C点下方,所以轨迹应为两段圆弧;通过以上分析可以作出图形,找到两种轨迹的交点,确定D点,求出AD即求出AP.
也为定值,利用定弦定角模型可知点D还应在圆弧上,因为点P可能在B点上方,还可能在C点下方,所以轨迹应为两段圆弧;通过以上分析可以作出图形,找到两种轨迹的交点,确定D点,求出AD即求出AP.
解:(1)相等;90°;
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
由旋转的性质可得:![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]()
∴![]()
即![]()
在![]() 与
与![]() 中,
中,
∵ ,
,
∴![]() ,
,
∴![]() ,
,![]()
∴![]()
(2)成立,证明如下:
如图②,连接![]() ,
,
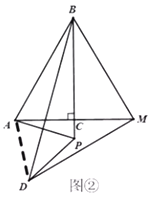
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
由旋转的性质可得:![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]()
∴![]() ,
,
在![]() 与
与![]() 中,
中,
∵ ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]()
(3)点P在直线BC上运动,由瓜豆原理可知,D点也应在直线上运动,在BC上选取两个特殊的P点位置,按照题意作出对应D点,然后连接点D所在直线确定;因为![]() 所以BM所对圆心角为60°,按照圆心在BM左侧和右侧两种情况,作出点D所在两端圆弧,直线与两端圆弧交点,即满足题意的点D,具体图形如下:
所以BM所对圆心角为60°,按照圆心在BM左侧和右侧两种情况,作出点D所在两端圆弧,直线与两端圆弧交点,即满足题意的点D,具体图形如下:
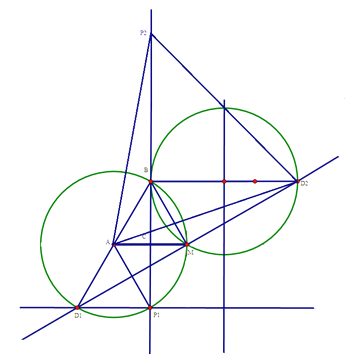
AP1=AD1=4;
AP2=AD2=![]()
综上所述,AP长为4或![]() .
.


科目:初中数学 来源: 题型:
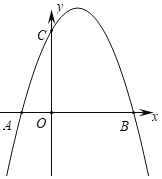
【题目】如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0),OB=OC=3OA.若抛物线L2与抛物线L1关于直线x=2对称.
(1)求抛物线L1与抛物线L2的解析式;
(2)在抛物线L1上是否存在一点P,在抛物线L2上是否存在一点Q,使得以BC为边,且以B、C、P、Q为顶点的四边形为平行四边形?若存在,求出P、Q两点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,直线y1=2x+4分别与x轴,y轴交于A,B两点,以线段OB为一条边向右侧作矩形OCDB,且点D在直线y2=﹣x+b上,若矩形OCDB的面积为20,直线y1=2x+4与直线y2=﹣x+b交于点P.则P的坐标为( )
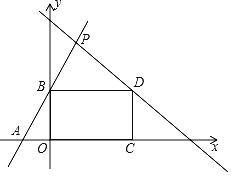
A.(2,8)B.![]() C.
C.![]() D.(4,12)
D.(4,12)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张大小、形状都相同的卡片上分别写有数字1,2,3,4,把它们放入不透明的盒子中摇匀.
(1)从中随机抽出1张卡片,抽出的卡片上的数字恰好是偶数的概率为 .
(2)从中随机抽出1张卡片,记录数字后放回摇匀,再抽出一张卡片,记录数字.用树状图或列表法求两次抽出的卡片上的数字恰好是两个相邻整数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
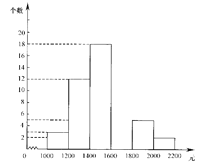
【题目】小明在“五一”假期间参加一项社会调查活动,在他所居住小区的600个家庭中,随机调查了50个家庭人均月收入情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).
分 组 | 频 数 | 频 率 |
1000~1200 | 3 | 0.060 |
1200~1400 | 12 | 0.240 |
1400~1600 | 18 | 0.360 |
1600~1800 | 0.200 | |
1800~2000 | 5 | |
2000~2200 | 2 | 0.040 |
合计 | 50 | 1.000 |
请你根据以上提供的信息,解答下列问题:
⑴ 补全频数分布表和频数分布直方图;
⑵ 这50个家庭人均月收入的中位数落在 小组;
⑶ 请你估算该小区600个家庭中人均月收入较低(不足1400元)的家庭个数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给抛物线y=a(x﹣h)2+k(a≠0)定义一种变换,先作这条抛物线关于原点对称的抛物线![]() ,再将得到的对称抛物线
,再将得到的对称抛物线![]() 向上平移m(m>0)个单位长度,得到新的抛物线ym,则我们称ym为二次函数y=a(x﹣h)2+k(a≠0)的m阶变换.若抛物线M的6阶变换的关系式为
向上平移m(m>0)个单位长度,得到新的抛物线ym,则我们称ym为二次函数y=a(x﹣h)2+k(a≠0)的m阶变换.若抛物线M的6阶变换的关系式为![]() .
.
(1)抛物线M的函数表达式为 ;
(2)若抛物线M的顶点为点A,与r轴相交的两个交点中的左侧交点为点B,则在抛物线![]() 上是否存在点P,使点P与直线AB的距离最短?若存在,请求出此时点P的坐标.
上是否存在点P,使点P与直线AB的距离最短?若存在,请求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com