
【题目】如图1,△ABC中,∠C=90°,若AC=6,BC=8,AD平分∠CAB交CB于D.
(1)求CD的长;
(2)如图2,E是AC上一点,连ED,过D作DE的垂线交AB于F,若ED=DF,求CE的长;
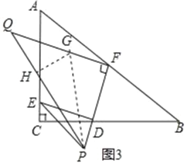
(3)如图3,在(2)条件下,点P在FD延长线上,过F作ED的平行线QF,连PE、PQ,若∠QPF=2∠PED=2α,PQ=5PD,(QF>PF),求QF.

【答案】(1)CD=3;(2)CE=1;(3)QF=![]() .
.
【解析】
(1)过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得CD=DE,利用勾股定理列式求出AB,然后根据S△ABC=S△ACD+S△ABD列方程求解即可.
(2)过F作FG⊥BC于G,证明:△CDE≌△GFD,△BGF∽△BCA,即可求解;
(3)过P作∠QPF的平分线交FQ于G,过G作GH⊥PQ于H,证明Rt△PFG≌Rt△PHG,△PED∽△GPF,设PD=x,建立方程求解即可.
(1)如图1,过点D作DE⊥AB于E,
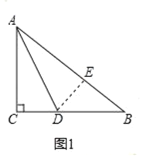
∵∠ACB=90°,AD平分∠CAB,
∴CD=DE,
在△ABC中由勾股定理得:AB=![]() =10,
=10,
∵S△ABC=S△ACD+S△ABD,
∴![]() ×AC×BC=
×AC×BC=![]() ×AC×CD+
×AC×CD+![]() ×AB×DE,即
×AB×DE,即![]() ×6×8=
×6×8=![]() ×6×CD+
×6×CD+![]() ×10×CD,
×10×CD,
解得:CD=3;
(2)如图2,过F作FG⊥BC于G,则∠C=∠FGD=90°,

∵DE⊥DF,
∴∠EDF=90°,
∴∠CDE+∠CED=∠CDE+∠FDG=90°,
∴∠CED=∠FDG,
在△CDE与△GFD中
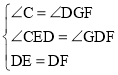 ,
,
∴△CDE≌△GFD(AAS),
∴CE=DG,FG=CD=3,
∵FG∥AC,
∴△BGF∽△BCA,
∴![]() =
=![]() ,
,
∴BG=4,
∴CE=DG=1;
(3)如图3,在Rt△CDE中,DE=DF=![]() =
=![]() ,
,
∵PQ=5PD,∴设PD=x,则PQ=5x,
∴PF=![]() +x,过P作∠QPF的平分线交FQ于G,过G作GH⊥PQ于H,
+x,过P作∠QPF的平分线交FQ于G,过G作GH⊥PQ于H,
∵FQ∥DE,∴∠QFP=∠EDP=90°,
∴GH=GF,在Rt△PFG与Rt△PHG中,![]() ,
,
∴Rt△PFG≌Rt△PHG(HL),
∴PH=PF=![]() +x,
+x,
∵∠QPF=2∠PED=2∠FPG=2α,
∴∠PED=∠FPG,
∴△PED∽△GPF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴FG=![]() ,
,
∴HG=FG=![]() ,
,
∵QH=PQ﹣PH=4x﹣![]() ,
,
∴QG=![]() ,FQ=QG+FG=
,FQ=QG+FG=![]() ,
,
∵△QGH∽△QPF
∴![]() =
=![]() ,即GHFQ=PFQG
,即GHFQ=PFQG
∴![]() ×
×![]() =(
=(![]() +x)×
+x)×![]() ,解得:x1=
,解得:x1=![]() (舍去),x2=
(舍去),x2=![]() ,
,
∴QF=![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3![]() ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )

A. (![]() ,
,![]() )B. (2,
)B. (2,![]() )C. (
)C. (![]() ,
,![]() )D. (
)D. (![]() ,3﹣
,3﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)

(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
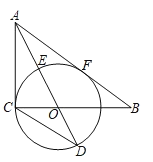
【题目】如图,在Rt△ABC中,∠ACB=90°,O是线段BC上一点,以O为圆心,OC为半径作⊙O,AB与⊙O相切于点F,直线AO交⊙O于点E,D.
(1)求证:AO是△CAB的角平分线;
(2)若tan∠D=![]() ,AE=2,求AC的长.
,AE=2,求AC的长.
(3)在(2)条件下,连接CF交AD于点G,⊙O的半径为3,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
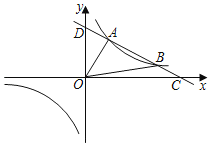
(1)求一次函数与反比例函数的解析式.
(2)求当x为何值时,y1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
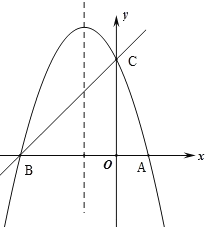
【题目】如图,已知抛物线![]() (a≠0)的对称轴为直线
(a≠0)的对称轴为直线![]() ,且抛物线经过A(1,0),C(0,3)两点,与
,且抛物线经过A(1,0),C(0,3)两点,与![]() 轴交于点B.
轴交于点B.
(1)若直线![]() 经过B,C两点,求直线BC和抛物线的解析式;
经过B,C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点M,使MA+MC的值最小,求点M的坐标;
上找一点M,使MA+MC的值最小,求点M的坐标;
(3)设P为抛物线的对称轴![]() 上的一个动点,求使ΔBPC为直角三角形的点P的坐标.
上的一个动点,求使ΔBPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,BA=AD=DC,点E在CB延长线上,BE=AD,连接AC、AE.

⑴ 求证:AE=AC;
⑵ 若AB⊥AC, F是BC的中点,试判断四边形AFCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
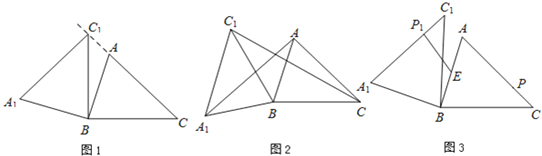
【题目】如图,在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为16,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com