
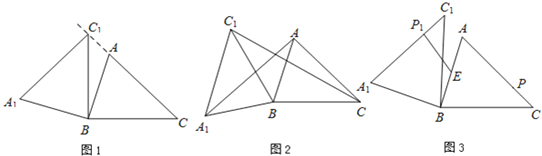
【题目】如图,在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为16,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值之和.
【答案】(1)90° (2)25 (3)![]()
【解析】
(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,又由等腰三角形的性质,即可求得∠CC1A1的度数;
(2)由旋转的性质可得:△ABC≌△A1BC1,易证得△ABA1∽△CBC1,利用相似三角形的面积比等于相似比的平方,即可求得△CBC1的面积;
(3)由①当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小;②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,即可求得线段EP1长度的最大值与最小值.
解:(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°;
(2)∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴![]() ,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
∴∠ABA1=∠CBC1,
∴△ABA1∽△CBC1,
∴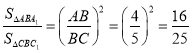 ,
,
∵S△ABA1=16,
∴S△CBC1=25;
(3)如图,过点B作BD⊥AC,D为垂足,
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin45°=![]() ;
;
①当P在AC上运动至BP⊥AC时,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1﹣BE=BD﹣BE=![]() ﹣2;
﹣2;
②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+BE=2+5=7;
因此,线段EP1长度的最大值与最小值的和为:7+![]() ﹣2=
﹣2=![]() .
.


科目:初中数学 来源: 题型:
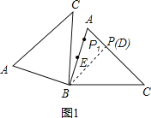
【题目】如图1,△ABC中,∠C=90°,若AC=6,BC=8,AD平分∠CAB交CB于D.
(1)求CD的长;
(2)如图2,E是AC上一点,连ED,过D作DE的垂线交AB于F,若ED=DF,求CE的长;
(3)如图3,在(2)条件下,点P在FD延长线上,过F作ED的平行线QF,连PE、PQ,若∠QPF=2∠PED=2α,PQ=5PD,(QF>PF),求QF.

查看答案和解析>>
科目:初中数学 来源: 题型:
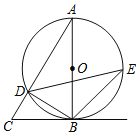
【题目】如图,已知△ABC中,以AB为直径的⊙O交AC于点D,∠CBD=∠A.
(1)求证:BC为⊙O的切线;
(2)若E为![]() 中点,BD=12,sin∠BED=
中点,BD=12,sin∠BED=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为m;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为n.
(1)用列表法或画树状图表示出(m,n)的所有可能出现的结果;
(2)小明认为点(m,n)在一次函数y=x+2的图象上的概率一定大于在反比例函数y=![]() 的图象上的概率,而小华却认为两者的概率相同.你赞成谁的观点?分别求出点(m,n)在两个函数图象上的概率,并说明谁的观点正确.
的图象上的概率,而小华却认为两者的概率相同.你赞成谁的观点?分别求出点(m,n)在两个函数图象上的概率,并说明谁的观点正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN=90°,点C在边AM上,AC=3,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
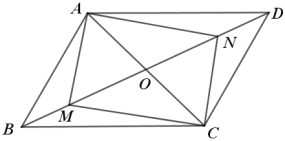
【题目】如图,已知平行四边形ABCD.
(1)若M,N是BD上两点,且BM=DN,AC=2OM,求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
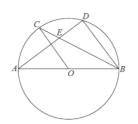
【题目】如图,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() ,
,![]() 为圆上的两点,
为圆上的两点,![]() ,弦
,弦![]() ,
,![]() 相交于点
相交于点![]() ,
,
(1)求证:![]()
(2)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交⊙
交⊙![]() 于
于![]() ,
, ![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),求
上),求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
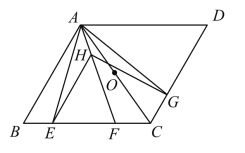
【题目】如图,在菱形ABCD中,AB=AC,点E、F、G分别在边BC、CD上,BE=CG,AF平分∠EAG,点H是线段AF上一动点(与点A不重合).
(1)求证:△AEH≌△AGH;
(2)当AB=12,BE=4时:
①求△DGH周长的最小值;
②若点O是AC的中点,是否存在直线OH将△ACE分成三角形和四边形两部分,其中三角形的面积与四边形的面积比为1:3.若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国淡水资源短缺问题十分突出,节约用水已成为各地的一件大事.某校初三学生为了调查居民用水情况,随机抽查了某小区10户家庭的月用水量,结果如表所示:
月用水量(t) | 3 | 4 | 5 | 10 |
户数 | 4 | 2 | 3 | 1 |
这10户家庭月用水量的平均数、中位数及众数是( )
A. 4.5,3,4B. 3,4.5,4C. 4.5,4,3D. 4,4.5,3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com