
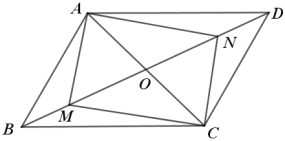
【题目】如图,已知平行四边形ABCD.
(1)若M,N是BD上两点,且BM=DN,AC=2OM,求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC,求平行四边形ABCD的面积.
【答案】(1)见解析;(2)16![]() .
.
【解析】
(1)由平行四边形的性质可知:OA=OC,OB=OD,再证明OM=ON即可证明四边形AMCN是平行四边形;
(2)根据平行四边形的性质得到AD∥BC,AB=CD=4,求得∠ABC=60°,解直角三角形即可得到结论.
(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=4,
∴∠BAD+∠ABC=180°,
∵∠BAD=120°,
∴∠ABC=60°,
∵AB⊥AC,
∴∠BAC=90°,
∴AC=![]() AB=4
AB=4![]() ,
,
∴平行四边形ABCD的面积=ACAB=4![]() 4=16
4=16![]() .
.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
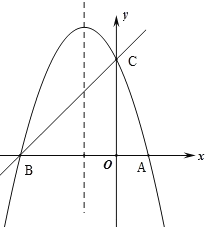
【题目】如图,已知抛物线![]() (a≠0)的对称轴为直线
(a≠0)的对称轴为直线![]() ,且抛物线经过A(1,0),C(0,3)两点,与
,且抛物线经过A(1,0),C(0,3)两点,与![]() 轴交于点B.
轴交于点B.
(1)若直线![]() 经过B,C两点,求直线BC和抛物线的解析式;
经过B,C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点M,使MA+MC的值最小,求点M的坐标;
上找一点M,使MA+MC的值最小,求点M的坐标;
(3)设P为抛物线的对称轴![]() 上的一个动点,求使ΔBPC为直角三角形的点P的坐标.
上的一个动点,求使ΔBPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
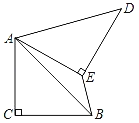
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则∠BED的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() 都是实数,且
都是实数,且![]() .我们规定:满足不等式
.我们规定:满足不等式![]() 的实数
的实数![]() 的所有值的全体叫做闭区间、表示为
的所有值的全体叫做闭区间、表示为![]() .对于一个函数,如果它的自变量
.对于一个函数,如果它的自变量![]() 与函数值
与函数值![]() 满足:当
满足:当![]() 时,有
时,有![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.
上的“闭函数”.
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此一次函数的解析式;
上的“闭函数”,求此一次函数的解析式;
(3)若实数![]() 满足
满足![]() .且
.且![]() ,当二次函数
,当二次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”时,求
上的“闭函数”时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
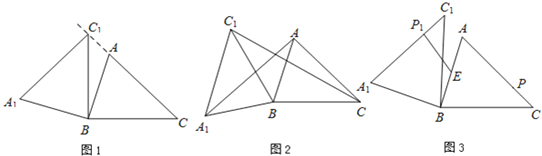
【题目】如图,在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为16,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“和谐号”列车缓缓停靠在梅州西站,我市正式进入了高铁时代.与普通列车相比,“和谐号”列车时速更快,安全性更好.已知“梅州西—广州南”全程大约![]() 千米,“和谐号”
千米,“和谐号”![]() 次列车平均每小时比普通列车多行驶
次列车平均每小时比普通列车多行驶![]() 千米,其行驶时间是普通列车行驶时间的
千米,其行驶时间是普通列车行驶时间的![]() (两列车中途停留时间均除外).
(两列车中途停留时间均除外).
(1)经查询,“和谐号”![]() 次列车从梅州西到广州南,中途合计停站时间为
次列车从梅州西到广州南,中途合计停站时间为![]() 分钟,求乘坐“和谐号”
分钟,求乘坐“和谐号”![]() 次列车从梅州西到广州南需要多长时间;
次列车从梅州西到广州南需要多长时间;
(2)据了解,梅州西站后期还会引进更快的“复兴号”高铁,届时跑完![]() 千米的路程最多只需要
千米的路程最多只需要![]() 小时,请问“复兴号”高铁的速度每小时至少比“和谐号”列车快了多少千米.
小时,请问“复兴号”高铁的速度每小时至少比“和谐号”列车快了多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
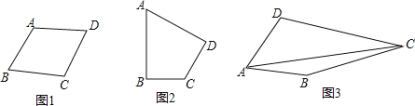
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
![]() 概念理解:
概念理解:
如图![]() ,在四边形
,在四边形![]() 中,添加一个条件使得四边形
中,添加一个条件使得四边形![]() 是“等邻边四边形”.请写出你添加的一个条件,你添加的条件是________.
是“等邻边四边形”.请写出你添加的一个条件,你添加的条件是________.
![]() 问题探究:
问题探究:
如图![]() ,在“等邻边四边形”
,在“等邻边四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,求对角线
,求对角线![]() 的长.
的长.
![]() 拓展应用:
拓展应用:
如图![]() ,“等邻边四边形”
,“等邻边四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为对角线,试探究
为对角线,试探究![]() ,
,![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(满分10分)已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
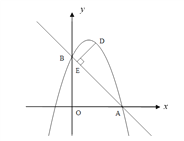
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,求直线AB与这个二次函数的解析式;
(3)在直线AB上方的抛物线上有一动点D,当D与直线AB的距离DE最大时,求点D的坐标,并求DE最大距离是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com