
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
![]() 概念理解:
概念理解:
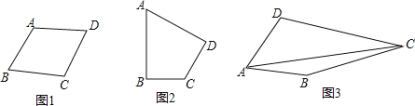
如图![]() ,在四边形
,在四边形![]() 中,添加一个条件使得四边形
中,添加一个条件使得四边形![]() 是“等邻边四边形”.请写出你添加的一个条件,你添加的条件是________.
是“等邻边四边形”.请写出你添加的一个条件,你添加的条件是________.
![]() 问题探究:
问题探究:
如图![]() ,在“等邻边四边形”
,在“等邻边四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,求对角线
,求对角线![]() 的长.
的长.
![]() 拓展应用:
拓展应用:
如图![]() ,“等邻边四边形”
,“等邻边四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为对角线,试探究
为对角线,试探究![]() ,
,![]() ,
,![]() 的数量关系.
的数量关系.
【答案】(1)![]() .(2)
.(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据定义可知:只需要一组邻边相等即可.
(2)由AB=AD,∠BAD=60°,可知△ABD是等边三角形,再由∠ABC=∠ADC=90°,可知CB=CD,所以AC垂直平分BD,然后利用直角三角形的相关性质分别计算出AO和OC的长度.
(3)由于∠BAD+∠BCD=90°,所以考虑构造直角三角形使得该直角三角形的三边长度分别是AC、BC、CD的长度,然后利用勾股定理即可得出AC2=BC2+CD2
(1)根据定义:AB=BC.
(2)连接AC、BD交于点O,如图,
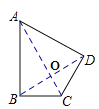
∵AB=AD,∠BAD=60°,
∴△ABD是等边三角形,
∴∠ABD=∠ADB=60°,
∵∠ABC=∠ADC=90°,
∴∠CBD=∠CDB=30°,
∴CB=CD,
∴AC垂直平分BD,
∴![]() ,
,
∴![]() ,
,
在Rt△BOC中,
![]() ,
,
∴OC=![]() ,
,
∴AC=AO+OC=4![]() ;
;
(3)过点C作CE⊥BC于点C,且使得CE=CD,

∵∠BAD+∠BCD=90°,
∴∠DCE=60°,
∴△CDE是等边三角形,
∴DE=CD,∠EDC=60°,
∵AB=AD,∠DAB=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
在△ADC和△BDE中,
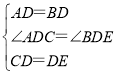 ,
,
∴△ADC≌△BDE(SAS),
∴AC=BE,
∵∠BCE=90°,
∴BE2=BC2+CE2,
即AC2=BC2+CD2


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可以合作施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
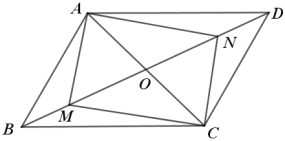
【题目】如图,已知平行四边形ABCD.
(1)若M,N是BD上两点,且BM=DN,AC=2OM,求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
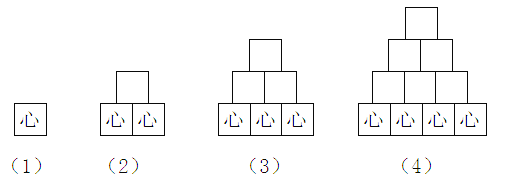
【题目】小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案(如图所示),每个图案中他只在最下面的正方体上写“心”字,寓意“不忘初心”.其中第(1)个图案中有1个正方体,第(2)个图案中有3个正方体,第(3)个图案中有6个正方体,……按照此规律,从第(100)个图案所需正方体中随机抽取一个正方体,抽到带“心”字正方体的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
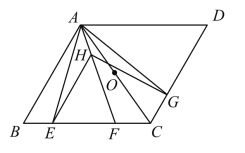
【题目】如图,在菱形ABCD中,AB=AC,点E、F、G分别在边BC、CD上,BE=CG,AF平分∠EAG,点H是线段AF上一动点(与点A不重合).
(1)求证:△AEH≌△AGH;
(2)当AB=12,BE=4时:
①求△DGH周长的最小值;
②若点O是AC的中点,是否存在直线OH将△ACE分成三角形和四边形两部分,其中三角形的面积与四边形的面积比为1:3.若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店经销甲、乙两种不同的笔记本.已知:两种笔记本的进价之和为10元,甲种笔记本每本获利2元,乙种笔记本每本获利1元,马阳光同学买4本甲种笔记本和3本乙种笔记本共用了47元.
(1)甲、乙两种笔记本的进价分别是多少元?
(2)该文具店购入这两种笔记本共60本,花费不超过296元,则购买甲种笔记本多少本时该文具店获利最大?
(3)店主经统计发现平均每天可售出甲种笔记本350本和乙种笔记本150本.如果甲种笔记本的售价每提高1元,则每天将少售出50本甲种笔记本;如果乙种笔记本的售价每提高1元,则每天少售出40本乙种笔记本,为使每天获取的利润更多,店主决定把两种笔记本的价格都提高![]() 元,在不考虑其他因素的条件下,当
元,在不考虑其他因素的条件下,当![]() 定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
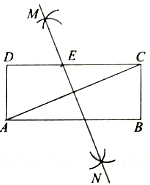
【题目】如图,在矩形![]() 中,小聪同学利用直尺和圆规完成了如下操作:
中,小聪同学利用直尺和圆规完成了如下操作:
①分别以点![]() 和
和![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() 和
和![]() ;
;
②作直线![]() ,交
,交![]() 于点
于点![]() .
.
请你观察图形解答下列问题:
(1)![]() 与
与![]() 的位置关系:
的位置关系:
直线![]() 是线段
是线段![]() 的____________线;
的____________线;
(2)若![]() ,
,![]() ,求矩形的对角线
,求矩形的对角线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将分别标有数字1,2,3的三张卡片(卡片除所标注数字外其他均相同)洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张,直接写出抽到的卡片所标数字是奇数的概率;
(2)随机地抽取一张,将卡片上标有的数字作为十位上的数字(不放回),再随机地抽取一张卡片,将卡片上标有的数字作为个位上的数字,用列表或树状图的方法求组成的两位数恰好是“32”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
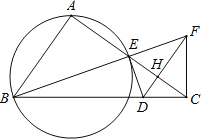
【题目】如图,Rt△ABC中,∠BAC=90°,E是AC的中点,AE=2.经过点E作△ABE外接圆的切线交BC于点D,过点C作CF⊥BC交BE的延长线于点F,连接FD交AC于点H,FD平分∠BFC.
(1)求证:DE=DC;
(2)求证:HE=HC=1;
(3)求BD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com