
【题目】如图,∠MAN=90°,点C在边AM上,AC=3,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为__.

科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
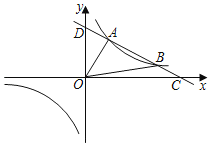
(1)求一次函数与反比例函数的解析式.
(2)求当x为何值时,y1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC.
【1】猜想:线段OD与BC有何数量和位置关系,并证明你的结论.
【2】求证:PC是⊙O的切线
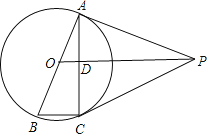
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC,BC是⊙O的两条弦,过点C作∠BCD=∠A,CD交AB的延长线于点D.
(1)试说明:CD是⊙O的切线;
(2)若tanA=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若AB=7,DE平分∠ADC交AC于点E,求ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°俯角(即望向屏幕中心P的的视线EP与水平线EA的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2)时,观看屏幕最舒适,此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为32cm.

(1)求眼睛E与显示屏顶端A的水平距离AE;(结果精确到1cm)
(2)求显示屏顶端A与底座C的距离AC.(结果精确到1cm)(参考数据:sin18°≈0.3,cos18°≈0.9,tan18°≈0.3,![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为16,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值之和.
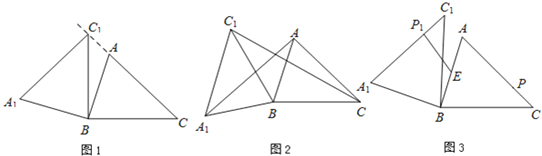
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了“防溺水”知识竞赛,八年级两个班选派10名同学参加预赛,依据各参赛选手的成绩(均为整数)绘制了统计表和折线统计图(如图所示).
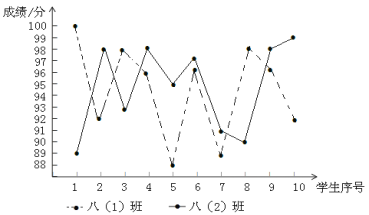
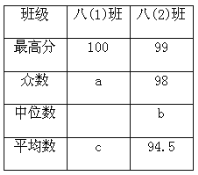
(1)统计表中,a=________, b =________;
(2)若从两个班的预赛选手中选四名学生参加决赛,其中两个班的第一名直接进入决赛,另外两个名额 在成绩为98分的学生中任选两个,求另外两个决赛名额落在不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
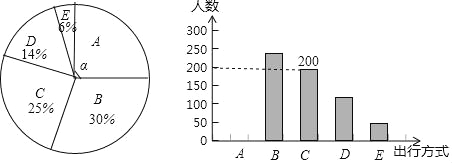
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com