
【题目】在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°俯角(即望向屏幕中心P的的视线EP与水平线EA的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2)时,观看屏幕最舒适,此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为32cm.

(1)求眼睛E与显示屏顶端A的水平距离AE;(结果精确到1cm)
(2)求显示屏顶端A与底座C的距离AC.(结果精确到1cm)(参考数据:sin18°≈0.3,cos18°≈0.9,tan18°≈0.3,![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
【答案】(1)约为53km;(2)约为34cm
【解析】
(1)由已知得![]() ,根据锐角三角函数即可求出眼睛E与显示屏顶端A的水平距离AE;
,根据锐角三角函数即可求出眼睛E与显示屏顶端A的水平距离AE;
(2)如图,过点B作BF⊥AC于点F,根据锐角三角函数求出AF和BF的长,进而求出显示屏顶端A与底座C的距离AC.
(1)由已知得![]() ,
,
在Rt△APE中,
∵![]() ,
,
∴![]() ,
,
答:眼睛E与显示屏顶端A的水平距离AE约为53km;
(2)如图,过点B作BF⊥AC于点F,
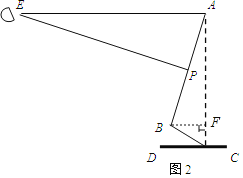
∵∠EAB+∠BAF=90°,∠EAB+∠AEP=90°,
∴∠BAF=∠AEP=18°,
在Rt△ABF中,
AF=ABcos∠BAF=32×cos18°≈32×0.9≈28.8,
BF=ABsin∠BAF=32×sin18°≈32×0.3≈9.6,
∵BF∥CD,
∴∠CBF=∠BCD=30°,
∴![]() ,
,
∴AC=AF+CF=28.8+5.44≈34(cm).
答:显示屏顶端A与底座C的距离AC约为34cm.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△EDF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
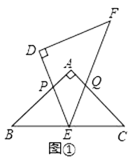
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
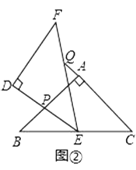
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;
(3)在(2)的条件下,BP=2,CQ=9,则BC的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
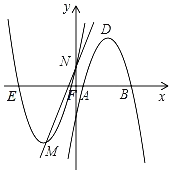
【题目】如图,在平面直角坐标系中,已知抛物线C1:y=![]() x2+6x+2的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2,直线l:y=kx+b经过M,N两点.
x2+6x+2的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2,直线l:y=kx+b经过M,N两点.
(1)求点M的坐标,并结合图象直接写出不等式![]() x2+6x+2<kx+b的解集;
x2+6x+2<kx+b的解集;
(2)若抛物线C2的顶点D与点M关于原点对称,求p的值及抛物线C2的解析式;
(3)若抛物线C1与x轴的交点为E、F,试问四边形EMBD是何种特殊四边形?并说明其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在向贫困地区捐书活动中全体师生积极捐书.为了解所捐书籍的种类,某同学对部分书籍进行了抽样调查,并根据调查数据绘制了如图所示不完整统计图.请根据统计图回答下面问题:
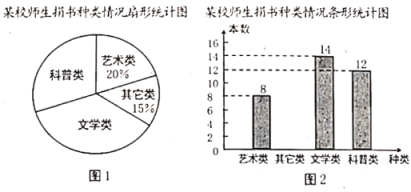
(1)本次抽样调查的书籍有多少本?请通过计算补全条形统计图;
(2)求出图![]() 中表示科普类书籍的扇形圆心角度数;
中表示科普类书籍的扇形圆心角度数;
(3)本次活动师生共捐书![]() 本,请估计有多少本文学类书籍?
本,请估计有多少本文学类书籍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠B=30°,且BC=CA,将△ABC沿AC翻折至△AB′C,AB′交CD于点E,连接B′D.若AB=3![]() ,则B′D的长度为______.
,则B′D的长度为______.
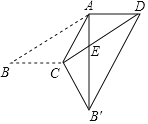
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN=90°,点C在边AM上,AC=3,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B在第一象限,BA⊥x轴于点A,反比例函数y=![]() (x>0)的图象与线段AB相交于点C,C是线段AB的中点,点C关于直线y=x的对称点C'的坐标为(m,6)(m≠6),若△OAB的面积为12,则k的值为( )
(x>0)的图象与线段AB相交于点C,C是线段AB的中点,点C关于直线y=x的对称点C'的坐标为(m,6)(m≠6),若△OAB的面积为12,则k的值为( )
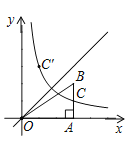
A.4B.6C.8D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供资源,待货物出售后再进行结算,未出售的由厂家负责处理)。当每吨售价为260元时,月销售量为45吨,该经销店为提高经营利润,准备采取降价的方式进行促销。经市场调查发现:当每吨售价每降低10元时,月销售量就会增加7.5吨,综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用![]() 元.
元.
![]() 当每吨售价为
当每吨售价为![]() 元时,月销售量为
元时,月销售量为![]() 吨,求出
吨,求出![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
![]() 在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为
在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为![]() 元;
元;
![]() 若在规定每吨售价不得超过
若在规定每吨售价不得超过![]() 元的情况下,当每吨售价定为多少元时,经销店的月利润最大.
元的情况下,当每吨售价定为多少元时,经销店的月利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com