
【题目】如图,在平行四边形ABCD中,∠B=30°,且BC=CA,将△ABC沿AC翻折至△AB′C,AB′交CD于点E,连接B′D.若AB=3![]() ,则B′D的长度为______.
,则B′D的长度为______.
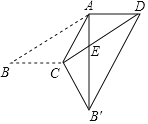
【答案】6
【解析】
作CM⊥AB于M,由折叠的性质得:B'C=BC=AC,∠AB'C=∠B=∠CAB'=30°,AB'=AB=CD,由平行四边形的性质得出AD=CB,AB=CD,∠ADC=∠B=30°,求出AD=AC,![]() ,∠BAC=∠B=30°,由等腰三角形的性质得出∠ACD=∠ADC=30°,由直角三角形的性质得出
,∠BAC=∠B=30°,由等腰三角形的性质得出∠ACD=∠ADC=30°,由直角三角形的性质得出![]() ,证出AD=BC=2CM=3,再由勾股定理即可得出结果.
,证出AD=BC=2CM=3,再由勾股定理即可得出结果.
解:作CM⊥AB于M,如图所示:
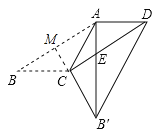
由折叠的性质得:B'C=BC=AC,∠AB'C=∠B=∠CAB'=30°,AB'=AB=CD,
∵四边形ABCD是平行四边形,
∴AD=CB,AB=CD,∠ADC=∠B=30°,∠BAD=∠BCD=180°-∠B=150°,
∴∠B'AD=150°-30°-30°=90°,
∵BC=AC,
∴![]() ,∠BAC=∠B=30°,
,∠BAC=∠B=30°,
∴![]() ,
,
∴AD=BC=2CM=3,
在Rt△AB'D中,由勾股定理得:B'D=![]() ;
;
故答案为:6.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△P1OA1,△P2A1A2,△P3A2A3,…都是等腰直角三角形,其直角顶点P1(3,3),P2,P3,…均在直线 ![]() 上.设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为 S1,S2,S3,…,依据图形所反映的规律,S2020=____.
上.设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为 S1,S2,S3,…,依据图形所反映的规律,S2020=____.

查看答案和解析>>
科目:初中数学 来源: 题型:
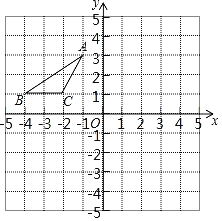
【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,A1的坐标为 ;
(2)再将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2画出△A1B2C2;
(3)求出在(2)的变换过程中,点B1到达点B2走过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
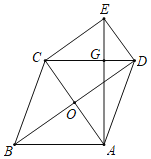
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,过点C作CE![]() BD,且CE=
BD,且CE=![]() BD.
BD.
(1)求证:四边形OCED是矩形;
(2)连接AE交CD于点G,若AE⊥CD.
①求sin∠CAG的值;
②若菱形ABCD的边长为6cm,点P为线段AE上一动点(不与点A重合),连接DP,一动点Q从点D出发,以1cm/s的速度沿线段DP匀速运动到点P,再以![]() cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动,当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间t.
cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动,当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间t.
查看答案和解析>>
科目:初中数学 来源: 题型:
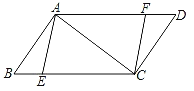
【题目】如图,在ABCD中,BC=10,对角线AC⊥AB,点EF在BC、AD上,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)当四边形AECF是菱形时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°俯角(即望向屏幕中心P的的视线EP与水平线EA的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2)时,观看屏幕最舒适,此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为32cm.

(1)求眼睛E与显示屏顶端A的水平距离AE;(结果精确到1cm)
(2)求显示屏顶端A与底座C的距离AC.(结果精确到1cm)(参考数据:sin18°≈0.3,cos18°≈0.9,tan18°≈0.3,![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春节过后受新冠肺炎的疫情影响,在线学习成为同学们学习的重要渠道.我校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
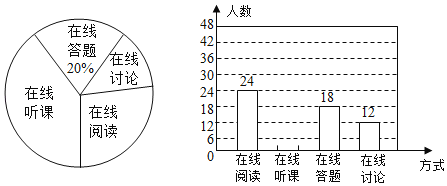
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生900人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以点A为圆心、AB的长为半径画弧交AD于点F,再分别以点B,F为圆心、大于![]() BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )
BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接EF.下列结论中不一定成立的是( )

A. BE=EFB. EF∥CDC. AE平分∠BEFD. AB=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com