
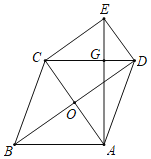
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌЙ§ЕуCзїCE![]() BDЃЌЧвCEЃН
BDЃЌЧвCEЃН![]() BDЃЎ
BDЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮOCEDЪЧОиаЮЃЛ
ЃЈ2ЃЉСЌНгAEНЛCDгкЕуGЃЌШєAEЁЭCDЃЎ
ЂйЧѓsinЁЯCAGЕФжЕЃЛ
ЂкШєСтаЮABCDЕФБпГЄЮЊ6cmЃЌЕуPЮЊЯпЖЮAEЩЯвЛЖЏЕуЃЈВЛгыЕуAжиКЯЃЉЃЌСЌНгDPЃЌвЛЖЏЕуQДгЕуDГіЗЂЃЌвд1cm/sЕФЫйЖШбиЯпЖЮDPдШЫйдЫЖЏЕНЕуPЃЌдйвд![]() cm/sЕФЫйЖШбиЯпЖЮPAдШЫйдЫЖЏЕНЕуAЃЌЕНДяЕуAКѓЭЃжЙдЫЖЏЃЌЕБЕуQбиЩЯЪіТЗЯпдЫЖЏЕНЕуAЫљашвЊЕФЪБМфзюЖЬЪБЃЌЧѓAPЕФГЄКЭЕуQзпЭъШЋГЬЫљашЕФЪБМфtЃЎ
cm/sЕФЫйЖШбиЯпЖЮPAдШЫйдЫЖЏЕНЕуAЃЌЕНДяЕуAКѓЭЃжЙдЫЖЏЃЌЕБЕуQбиЩЯЪіТЗЯпдЫЖЏЕНЕуAЫљашвЊЕФЪБМфзюЖЬЪБЃЌЧѓAPЕФГЄКЭЕуQзпЭъШЋГЬЫљашЕФЪБМфtЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШжЄУїЫФБпаЮOCEDЪЧЦНааЫФБпаЮЃЌдйИљОнЁЯCODЃН90ЁуЭЦГіЪЧОиаЮЃЎ
ЃЈ2ЃЉЂйгЩDEЁЮACЃЌDEЃНOCЃНOAЃЌЭЦГі![]() ЃЌЩшDGЃНmЃЌдђCGЃН2mЃЌDCЃНADЃН3mЃЌЧѓГіACМДПЩНтОіЮЪЬтЃЎ
ЃЌЩшDGЃНmЃЌдђCGЃН2mЃЌDCЃНADЃН3mЃЌЧѓГіACМДПЩНтОіЮЪЬтЃЎ
ЂкЙ§ЕуPзїPTЁЭACгкTЃЎгЩsinЁЯPATЃН![]() ЃЌЭЦГіPTЃН
ЃЌЭЦГіPTЃН![]() PAЃЌгЩЕуQЕФдЫЖЏЪБМфtЃН
PAЃЌгЩЕуQЕФдЫЖЏЪБМфtЃН![]() ЃНPD+PTЃЌИљОнДЙЯпЖЮзюЖЬПЩжЊЃЌЕБDЃЌPЃЌTЙВЯпЃЌЧвDTЁЭACЪБЃЌPD+PTЕФжЕзюаЁЃЌзюаЁжЕЃНЯпЖЮODЕФГЄЃЎ
ЃНPD+PTЃЌИљОнДЙЯпЖЮзюЖЬПЩжЊЃЌЕБDЃЌPЃЌTЙВЯпЃЌЧвDTЁЭACЪБЃЌPD+PTЕФжЕзюаЁЃЌзюаЁжЕЃНЯпЖЮODЕФГЄЃЎ
ЃЈ1ЃЉжЄУїЃКЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрACЁЭBDЃЌOBЃНODЃЌ
ЁпECЃН![]() BDЃЌ
BDЃЌ
ЁрECЃНODЃЌ
ЁпECЁЮODЃЌ
ЁрЫФБпаЮOCEDЪЧЦНааЫФБпаЮЃЌ
ЁпЁЯCODЃН90ЁуЃЌ
ЁрЫФБпаЮOCEDЪЧОиаЮЃЎ
ЃЈ2ЃЉНтЃКЂйЁпЫФБпаЮOCEDЪЧОиаЮЃЌ
ЁрDEЁЮACЃЌDEЃНOCЃНOAЃЌ
Ёр![]() ЃЌЩшDGЃНmЃЌдђCGЃН2mЃЌDCЃНADЃН3mЃЌ
ЃЌЩшDGЃНmЃЌдђCGЃН2mЃЌDCЃНADЃН3mЃЌ
ЁпAEЁЭCDЃЌ
ЁрЁЯAGDЃНЁЯAGCЃН90ЁуЃЌ
ЁрAGЃН![]() ЃЌ
ЃЌ
ЁрACЃН![]() ЃЌ
ЃЌ
ЁрsinЁЯCAGЃН![]() ЃЎ
ЃЎ
ЂкЙ§ЕуPзїPTЁЭACгкTЃЎ
ЁпsinЁЯPATЃН![]() ЃЌ
ЃЌ
ЁрPTЃН![]() PAЃЌ
PAЃЌ
ЁпЕуQЕФдЫЖЏЪБМфtЃН![]() ЃНPD+PTЃЌ
ЃНPD+PTЃЌ
ИљОнДЙЯпЖЮзюЖЬПЩжЊЃЌЕБDЃЌPЃЌTЙВЯпЃЌЧвDTЁЭACЪБЃЌPD+PTЕФжЕзюаЁЃЌзюаЁжЕЃНЯпЖЮODЕФГЄЃЌ
гЩЃЈ2ЃЉПЩжЊ3mЃН6ЃЌ
mЃН2ЃЌ
ЁрACЃН![]() ЃЌOAЃН
ЃЌOAЃН![]() ЃЌ
ЃЌ
ЁпЁЯAODЃН90ЁуЃЌ
ЁрODЃН![]() ЃЌ
ЃЌ
ЁпDEЁЮOAЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрOPЃНPDЃН![]() ЃЌДЫЪБAPЃН
ЃЌДЫЪБAPЃН![]() ЃЌ
ЃЌ
ЁрТњзуЬѕМўЕФPAЕФжЕЮЊ![]() ЃЌЕуQзпЭъШЋГЬЫљашЕФЪБМфtЃН
ЃЌЕуQзпЭъШЋГЬЫљашЕФЪБМфtЃН![]() ЃЈsЃЉЃЎ
ЃЈsЃЉЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
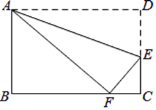
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=3ЃЌAD=5ЃЌЕуEдкDCЩЯЃЌНЋОиаЮABCDбиAEелЕўЃЌЕуDЧЁКУТфдкBCБпЩЯЕФЕуFДІЃЌФЧУДsinЁЯEFCЕФжЕЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌвбжЊAЃЈ0ЃЌ1ЃЉЃЌBЃЈ10ЃЌ1ЃЉЃЌCЃЈ9ЃЌ4ЃЉЃЎ

ЃЈ1ЃЉдкЭјИёжаЛГіЙ§AЁЂBЁЂCШ§ЕуЕФдВКЭжБЯп![]() ЕФЭМЯёЃЛ
ЕФЭМЯёЃЛ
ЃЈ2ЃЉвбжЊPЪЧжБЯп![]() ЩЯЕФЕуЃЌЧвЁїAPBЪЧжБНЧШ§НЧаЮЃЌФЧУДЗћКЯЬѕМўЕФЕуPЙВга ИіЃЛ
ЩЯЕФЕуЃЌЧвЁїAPBЪЧжБНЧШ§НЧаЮЃЌФЧУДЗћКЯЬѕМўЕФЕуPЙВга ИіЃЛ
ЃЈ3ЃЉШчЙћжБЯп![]() ЃЈk>0ЃЉЩЯгаЧвжЛгаЖўИіЕуQгыЕуAЁЂЕуBСНЕуЙЙГЩжБНЧЁїABQЃЌдђkЃН ЃЎ
ЃЈk>0ЃЉЩЯгаЧвжЛгаЖўИіЕуQгыЕуAЁЂЕуBСНЕуЙЙГЩжБНЧЁїABQЃЌдђkЃН ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
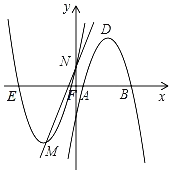
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯпC1ЃКyЃН![]() x2+6x+2ЕФЖЅЕуЮЊMЃЌгыyжсЯрНЛгкЕуNЃЌЯШНЋХзЮяЯпC1биxжсЗелЃЌдйЯђгвЦНвЦpИіЕЅЮЛГЄЖШКѓЕУЕНХзЮяЯпC2ЃЌжБЯпlЃКyЃНkx+bОЙ§MЃЌNСНЕуЃЎ
x2+6x+2ЕФЖЅЕуЮЊMЃЌгыyжсЯрНЛгкЕуNЃЌЯШНЋХзЮяЯпC1биxжсЗелЃЌдйЯђгвЦНвЦpИіЕЅЮЛГЄЖШКѓЕУЕНХзЮяЯпC2ЃЌжБЯпlЃКyЃНkx+bОЙ§MЃЌNСНЕуЃЎ
ЃЈ1ЃЉЧѓЕуMЕФзјБъЃЌВЂНсКЯЭМЯѓжБНгаДГіВЛЕШЪН![]() x2+6x+2ЃМkx+bЕФНтМЏЃЛ
x2+6x+2ЃМkx+bЕФНтМЏЃЛ
ЃЈ2ЃЉШєХзЮяЯпC2ЕФЖЅЕуDгыЕуMЙигкдЕуЖдГЦЃЌЧѓpЕФжЕМАХзЮяЯпC2ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШєХзЮяЯпC1гыxжсЕФНЛЕуЮЊEЁЂFЃЌЪдЮЪЫФБпаЮEMBDЪЧКЮжжЬиЪтЫФБпаЮЃПВЂЫЕУїЦфРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПRtЁїABCжаЃЌABЃНACЃЌDЕуЮЊRtЁїABCЭтвЛЕуЃЌЧвBDЁЭCDЃЌDFЮЊЁЯBDAЕФЦНЗжЯпЃЌЕБЁЯACDЃН15ЁуЃЌЯТСаНсТлЃКЂйЁЯADCЃН45ЁуЃЛЂкADЃНAFЃЛЂлAD+AFЃНBDЃЛЂмBCЉCEЃН2D,Цфжае§ШЗЕФЪЧ( )

A.ЂйЂлB.ЂйЂкЂмC.ЂйЂлЂмD.ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃдкЯђЦЖРЇЕиЧјОшЪщЛюЖЏжаШЋЬхЪІЩњЛ§МЋОшЪщ.ЮЊСЫНтЫљОшЪщМЎЕФжжРрЃЌФГЭЌбЇЖдВПЗжЪщМЎНјааСЫГщбљЕїВщЃЌВЂИљОнЕїВщЪ§ОнЛцжЦСЫШчЭМЫљЪОВЛЭъећЭГМЦЭМ.ЧыИљОнЭГМЦЭМЛиД№ЯТУцЮЪЬтЃК
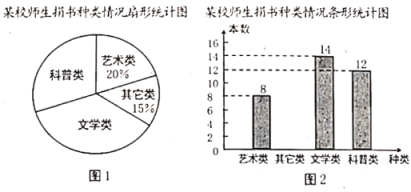
ЃЈ1ЃЉБОДЮГщбљЕїВщЕФЪщМЎгаЖрЩйБОЃПЧыЭЈЙ§МЦЫуВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉЧѓГіЭМ![]() жаБэЪОПЦЦеРрЪщМЎЕФЩШаЮдВаФНЧЖШЪ§ЃЛ
жаБэЪОПЦЦеРрЪщМЎЕФЩШаЮдВаФНЧЖШЪ§ЃЛ
ЃЈ3ЃЉБОДЮЛюЖЏЪІЩњЙВОшЪщ![]() БОЃЌЧыЙРМЦгаЖрЩйБОЮФбЇРрЪщМЎЃП
БОЃЌЧыЙРМЦгаЖрЩйБОЮФбЇРрЪщМЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌЁЯBЃН30ЁуЃЌЧвBCЃНCAЃЌНЋЁїABCбиACЗелжСЁїABЁфCЃЌABЁфНЛCDгкЕуEЃЌСЌНгBЁфDЃЎШєABЃН3![]() ЃЌдђBЁфDЕФГЄЖШЮЊ______ЃЎ
ЃЌдђBЁфDЕФГЄЖШЮЊ______ЃЎ
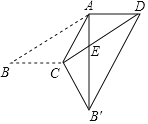
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуBдкЕквЛЯѓЯоЃЌBAЁЭxжсгкЕуAЃЌЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓгыЯпЖЮABЯрНЛгкЕуCЃЌCЪЧЯпЖЮABЕФжаЕуЃЌЕуCЙигкжБЯпyЃНxЕФЖдГЦЕуC'ЕФзјБъЮЊЃЈmЃЌ6ЃЉЃЈmЁй6ЃЉЃЌШєЁїOABЕФУцЛ§ЮЊ12ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЃЈxЃО0ЃЉЕФЭМЯѓгыЯпЖЮABЯрНЛгкЕуCЃЌCЪЧЯпЖЮABЕФжаЕуЃЌЕуCЙигкжБЯпyЃНxЕФЖдГЦЕуC'ЕФзјБъЮЊЃЈmЃЌ6ЃЉЃЈmЁй6ЃЉЃЌШєЁїOABЕФУцЛ§ЮЊ12ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
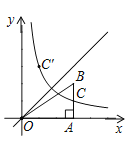
A.4B.6C.8D.12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌEЮЊCDЕФжаЕуЃЌСЌНгAEВЂбгГЄНЛBCЕФбгГЄЯпгкЕуFЃЌСЌНгBDНЛAFгкHЃЌAD=10![]() ЃЌЧвtanЁЯEFC=
ЃЌЧвtanЁЯEFC=![]() ЃЌФЧУДAHЕФГЄЮЊЃЈЁЁЁЁЃЉ
ЃЌФЧУДAHЕФГЄЮЊЃЈЁЁЁЁЃЉ
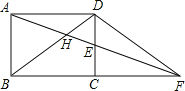
A. ![]() B.
B. ![]() C. 10D. 5
C. 10D. 5
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com