
【题目】如图,梯形ABCD中,AD∥BC,BA=AD=DC,点E在CB延长线上,BE=AD,连接AC、AE.

⑴ 求证:AE=AC;
⑵ 若AB⊥AC, F是BC的中点,试判断四边形AFCD的形状,并说明理由.
【答案】(1)见解析;(2)四边形AFCD是菱形,理由见解析
【解析】
(1)首先连接BD,根据等腰梯形的性质,可得AC=BD,易得四边形AEBD是平行四边形,由平行四边形的对边相等,即可得AE=BD,继而证得结论;
(2)由AB⊥AC,F是BC的中点,根据等腰梯形的性质,易求得∠ACB=30°,继而可证得AF=FC=CD=AD,则可判定四边形AFCD是菱形.
(1)连接BD
∵梯形ABCD是等腰梯形
∴AC=BD
∵BE=AD, AD∥BC
∴四边形AEBD是平行四边形
∴AE=BD,
∴AE=AC
(2)四边形AFCD是菱形, 理由是:
∵AB⊥AC, F是BC的中点
∴AF=CF,
∴∠FAC=∠FCA
∵AD=DC,
∴∠DAC=∠DCA
∵AD∥BC,
∴∠DAC=∠FCA
∴∠DCA=∠FAC
∴AF∥DC
∵AD∥BC,AF∥DC
∴四边形AFCD是平行四边形
又AD=DC
∴四边形AFCD是菱形


科目:初中数学 来源: 题型:
【题目】为有效解决交通拥堵问题,营造路网微循环,某市决定对一条长![]() 的道路进行改造拓宽.为了尽量减轻施工对城市交通造成的影响,实际施工时,每天改造道路的长度比原计划增加
的道路进行改造拓宽.为了尽量减轻施工对城市交通造成的影响,实际施工时,每天改造道路的长度比原计划增加![]() ,结果提前
,结果提前![]() 天完成任务,求实际每天改造道路的长度与实际施工天数.嘉琪同学根据题意列出方程
天完成任务,求实际每天改造道路的长度与实际施工天数.嘉琪同学根据题意列出方程![]() ,则方程中未知数
,则方程中未知数![]() 所表示的量是( )
所表示的量是( )
A.实际每天改造道路的长度B.原计划每天改造道路的长度
C.原计划施工的天数D.实际施工的天数
查看答案和解析>>
科目:初中数学 来源: 题型:
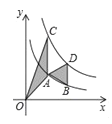
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,![]() .,已知点A,B的横坐标分别为1、2,△OAC与△ABD的面积之和为3,则k的值为( )
.,已知点A,B的横坐标分别为1、2,△OAC与△ABD的面积之和为3,则k的值为( )
A.5B.4C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,∠C=90°,若AC=6,BC=8,AD平分∠CAB交CB于D.
(1)求CD的长;
(2)如图2,E是AC上一点,连ED,过D作DE的垂线交AB于F,若ED=DF,求CE的长;
(3)如图3,在(2)条件下,点P在FD延长线上,过F作ED的平行线QF,连PE、PQ,若∠QPF=2∠PED=2α,PQ=5PD,(QF>PF),求QF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,对△ABC 进行循环往复的轴对称或中心对称变换,若原来点 A 坐标是(a,b),则经过第 2012 次变换后所得的 A 点坐标是( )
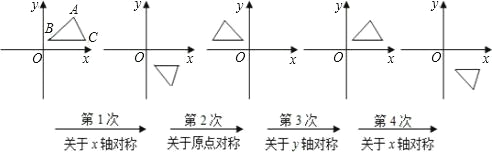
A. (a,b) B. (a,﹣b) C. (﹣a,b) D. (﹣a,﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
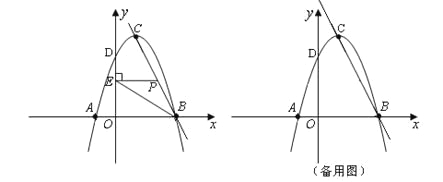
【题目】如图,在直角坐标系中,抛物线![]() 与y轴交于点D(0,3).
与y轴交于点D(0,3).
(1)直接写出c的值;
(2)若抛物线与x轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
(3)已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥y轴,垂足为E,连结BE.设点P的坐标为(x,y),△PBE的面积为s,求s与x的函数关系式,写出自变量x的取值范围,并求出s的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为r的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求r的值,并直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
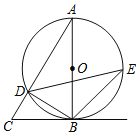
【题目】如图,已知△ABC中,以AB为直径的⊙O交AC于点D,∠CBD=∠A.
(1)求证:BC为⊙O的切线;
(2)若E为![]() 中点,BD=12,sin∠BED=
中点,BD=12,sin∠BED=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
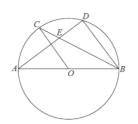
【题目】如图,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() ,
,![]() 为圆上的两点,
为圆上的两点,![]() ,弦
,弦![]() ,
,![]() 相交于点
相交于点![]() ,
,
(1)求证:![]()
(2)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交⊙
交⊙![]() 于
于![]() ,
, ![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),求
上),求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com