
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求抛物线的表达式;
(2)抛物线![]() 在第一象限内的部分记为图象
在第一象限内的部分记为图象![]() ,如果过点
,如果过点![]() 的直线
的直线![]() 与图象
与图象![]() 有唯一公共点,请结合图象,求
有唯一公共点,请结合图象,求![]() 的取值范围.
的取值范围.

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)将点![]() 坐标代入二次函数解析式即可求得;
坐标代入二次函数解析式即可求得;
(2)如图,先求出直线![]() 解析式,从而知其与
解析式,从而知其与![]() 轴的交点
轴的交点![]() ,由图象知过点
,由图象知过点![]() 的直线与
的直线与![]() 轴交点在
轴交点在![]() (含点
(含点![]() ,不含点
,不含点![]() )之间时,与图象
)之间时,与图象![]() 有唯一公共点,据此解答可得.
有唯一公共点,据此解答可得.
解:(1)将![]() 两点的坐标代入抛物线的表达式中,
两点的坐标代入抛物线的表达式中,
得:![]() ,解得
,解得![]() ,
,
∴抛物线的表达式为![]() ;
;
(2)设抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,则点
,则点![]() 的坐标为(0,3),
的坐标为(0,3),
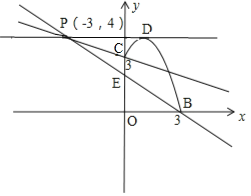
抛物线![]() 的顶点坐标为(1,4),
的顶点坐标为(1,4),
设直线![]() 解析式为
解析式为![]() ,
,
将点![]() 代入,得:
代入,得:![]() ,
,
解得: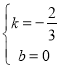 ,
,
∴直线![]() 的表达式为
的表达式为![]() ,
,
∴与![]() 轴交于点
轴交于点![]() ,
,
∵直线![]() 平行于
平行于![]() 轴,
轴,
∴与![]() 轴交于点
轴交于点![]() ,
,
由图象可知,当过点![]() 的直线与
的直线与![]() 轴交点在
轴交点在![]() (含点
(含点![]() ,不含点
,不含点![]() )之间时,与图象
)之间时,与图象![]() 有唯一公共点,
有唯一公共点,
另外,直线![]() 与图象
与图象![]() 也有唯一公共点,
也有唯一公共点,
但此时![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
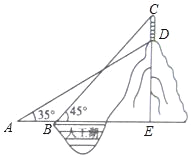
【题目】某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC,A点的坐标为(5,0),对角线OB、AC相交于D点,双曲线y=![]() (x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OBAC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6
(x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OBAC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6![]() ;④S△AFM:S△AOM=1:3.其中正确的结论是( )
;④S△AFM:S△AOM=1:3.其中正确的结论是( )

A. ①②B. ①③C. ①②③D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+l与双曲线y=![]() 的一个交点为A(m,-3).
的一个交点为A(m,-3).
(1)求双曲线的表达式;
(2)过动点P(n,0)(n<0)且垂直于x轴的直线与直线y=2x+l和双曲线y=![]() 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值,求m的值;
x | … |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | … |
y | … |
|
|
|
|
|
|
|
|
|
| m | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第二象限内的最低点的坐标是![]() ,结合函数的图象,写出该函数的其它性质(一条即可) .
,结合函数的图象,写出该函数的其它性质(一条即可) .
(5)根据函数图象估算方程![]() 的根为 .(精确到0.1)
的根为 .(精确到0.1)
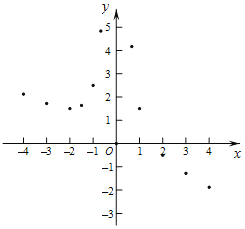
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
社会消费品零售总额是指批发和零售业,住宿和餐饮业以及其他行业直接售给城乡居民和社会集团的消费品零售额,在各类与消费有关的统计数据中,社会消费品零售总额是表现国内消费需求最直接的数据.
2012年,北京市全年实现社会消费品零售总额7702.8亿元,比上一年增长11.6%,2013年,全年实现社会消费品零售总额8375.1亿元,比上一年增长8.7%,2014年,全年实现社会消费品零售总额9098.1亿元,比上一年增长8.6%,2015年,全年实现社会消费品零售总额10338亿元,比上一年增长7.3%.
2016年,北京市实现市场总消费19926.2亿元,比上一年增长了8.1%,其中实现服务性消费8921.1亿元,增长10.1%;实现社会消费品零售总额11005.1亿元,比上一年增长了6.5%.
根据以上材料解答下列问题:
(1)补全统计表:
2012﹣2016年北京市社会消费品零售总额统计表
年份 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 |
社会消费品零售总额(单位:亿元) | ____ | _____ | _____ | _____ | _____ |
(2)选择适当的统计图将2012﹣2016年北京市社会消费品零售总额比上一年的增长率表示出来,并在图中表明相应数据;
(3)根据以上信息,估计2017年北京市社会消费品零售总额比上一年的增长率约为_________,你的预估理由是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大小为![]() 的正方形方格中,线段
的正方形方格中,线段![]() 的两端点都在单位小正方形的顶点上.
的两端点都在单位小正方形的顶点上.
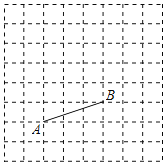
(1)在方格中画出一个![]() ,点
,点![]() 在小正方形的格点上使得
在小正方形的格点上使得![]() ,
,![]() .
.
(2)在方格中画出一个等腰![]() ,点
,点![]() 在小正方形的格点上,且使顶角为钝角,其面积等于4.
在小正方形的格点上,且使顶角为钝角,其面积等于4.
(3)在(1)(2)的条件下,连接![]() ,四边形
,四边形![]() 的面积为______个面积单位.
的面积为______个面积单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
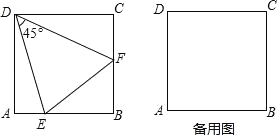
【题目】如图,在正方形 ABCD 中,E 为直线 AB 上的动点(不与 A、B 重合),作射线 DE 并绕点 D 逆时针旋转 45°,交直线 BC 于点 F,连接 EF.
探究:当点 E 在边 AB 上,求证:EF=AE+CF.
应用:(1)当点 E 在边 AB 上,且 AD=2 时,求△BEF 的周长;
(2)当点 E 在 BA 延长线上时,判断 EF,AE,CF 三者的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1 = x2 + 2x + 2与y2 = x2 - 2x + 2是“关于y轴对称二次函数”.
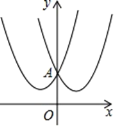
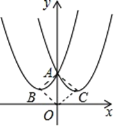
(1)二次函数y = 2(x + 2)2 + 1的“关于y轴对称二次函数”解析式为 ;二次函数y = a(x - h)2 + k的“关于y轴对称二次函数”解析式为 ;
(2)如备用图,平面直角坐标系中,记“关于y轴对称二次函数”的图象与y轴的交点为A,它们的两个顶点分别为B,C,且BC=6,顺次连接点A,B,O,C得到一个面积为24的菱形,求“关于y轴对称二次函数”的函数表达式.
(3)在第(2)题的情况下,如果M是两个抛物线上的一点,以点A,O,C,M为顶点能否构成梯形. 若能,求出此时M坐标;若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com