
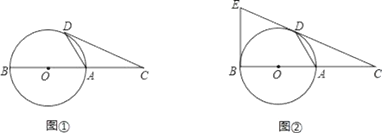
【题目】已知点C为直径BA的延长线上一点,CD切⊙O于点D,
(Ⅰ)如图①,若∠CDA=26°,求∠DAB的度数;
(Ⅱ)如图②,过点B作⊙O的切线交CD的延长线于点E,若⊙O的半径为3,BC=10,求BE的长.
【答案】(I)∠DAB =64°;(II) BE的长是![]()
【解析】
(I)根据切线的性质得出∠ODC=90°,求出∠ODA,根据等腰三角形的性质求出即可;
(II)根据切线长定理得出BE=DE,根据勾股定理求出DC,根据勾股定理得出方程,求出方程的解即可.
(I)如图①,连接OD,
∵CD切⊙O于点D,
∴∠ODC=90°,
∴∠CDA+∠ODA=90°,
∵∠CDA=26°,
∴∠ADO=64°,
∵OD=OA,
∴∠DAB=∠ODA=64°;
(II)如图②,连接OD,
在Rt△ODC中,OC=BCOB=103=7,
![]()
∵ED、EB分别为⊙O的切线,
∴ED=EB,
在Rt△CBE中,设BE=x,由![]() 得:
得:![]()
解得:![]()
∴BE的长是![]()



科目:初中数学 来源: 题型:
【题目】把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )

A. 6→3 B. 7→16 C. 7→8 D. 6→15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
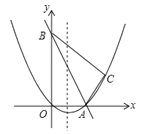
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
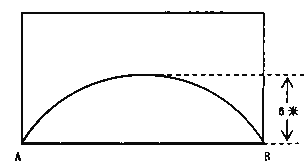
【题目】为了实现省城合肥跨越发展,近两年我市开始全面实施“畅通一环”工程,如图为一环路的一座下穿路拱桥,它轮廓是抛物线,桥的跨度AB=16米,拱高为6米.
(1)请以A点为坐标原点,AB所在直线为x轴建立平面直角坐标系,将抛物线放在直角坐标系中,求出抛物线的解析式;
(2)若桥拱下是双向行车道,其中一条行车道能否并排行驶宽3米,高2米的两辆汽车(汽车间隔不小于1米)说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,已知正比例函数 y1=﹣2x 的图象与反比例函数 y2=![]() 的图象交于 A(﹣1,a),B 两点.
的图象交于 A(﹣1,a),B 两点.
(1)求出反比例函数的解析式及点 B 的坐标;
(2)观察图象,请直接写出满足 y≤2 的取值范围;
(3)点 P 是第四象限内反比例函数的图象上一点,若△POB 的面积为 1,请直接写出点 P的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
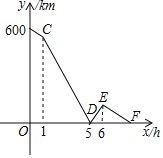
【题目】A、B两地之间为直线距离且相距600千米,甲开车从A地出发前往B地,乙骑自行车从B地出发前往A地,已知乙比甲晚出发1小时,两车均匀速行驶,当甲到达B地后立即原路原速返回,在返回途中再次与乙相遇后两车都停止,如图是甲、乙两人之间的距离s(千类)与甲出发的时间t(小时)之间的图象,则当甲第二次与乙相遇时,乙离B地的距离为_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
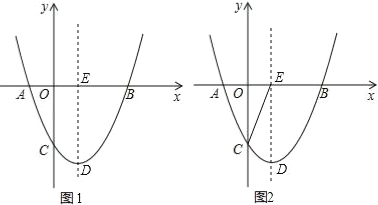
【题目】如图1,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣2),顶点为D,对称轴交x轴于点E.
(1)求该二次函数的解析式;
(2)设M为该抛物线对称轴左侧上的一点,过点M作直线MN∥x轴,交该抛物线于另一点N.是否存在点M,使四边形DMEN是菱形?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)连接CE(如图2),设点P是位于对称轴右侧该抛物线上一点,过点P作PQ⊥x轴,垂足为Q.连接PE,请求出当△PQE与△COE相似时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创建“全国文明城市”和“省级文明城区”过程中,栾城区污水处理厂决定先购买A、B两型污水处理设备共20台,对城区周边污水进行处理.已知每台A型设备价格为12万元,每台B型设备价格为10万元;1台A型设备和2台B型设备每周可以处理污水640吨,2台A型设备和3台B型设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)要想使污水处理厂购买设备的资金不超过230万元,但每周处理污水的量又不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.

(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留π和根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com