
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
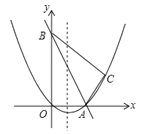
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ,直角三角形;(2)
,直角三角形;(2)![]() ;(3)M1(
;(3)M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() ).
).
【解析】
(1)先确定出点A,B坐标,再用待定系数法求出抛物线解析式;用勾股定理逆定理证出AC2+BC2=AB2,则△ABC是直角三角形;
(2)根据运动表示出OP=2t,CQ=10﹣t,由已知条件证明Rt△AOP≌Rt△ACQ,得到OP=CQ即可;
(3)分当BM=BA,AM=AB,MA=MB三种情况分类讨论,由两点间的距离公式计算即可,
解:(1)∵直线y=﹣2x+10与x轴,y轴相交于A,B两点,
∴A(5,0),B(0,10),
∵抛物线过原点,
∴设抛物线解析式为y=ax2+bx,
∵抛物线过点A(5,0),C(8,4),
∴![]() ,∴
,∴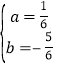 ,
,
∴抛物线解析式为y=![]() x2﹣
x2﹣![]() x,
x,
∵A(5,0),B(0,10),C(8,4),
∴AB2=52+102=125,BC2=82+(10﹣4)2=100,AC2=42+(8﹣5)2=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
(2)如图1,
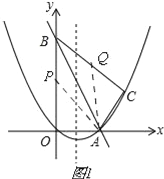
当P,Q运动t秒,即OP=2t,CQ=10﹣t时,
由(1)得,AC=OA,∠ACQ=∠AOP=90°,
在Rt△AOP和Rt△ACQ中,
AC=OA,PA=QA,
∴Rt△AOP≌Rt△ACQ,
∴OP=CQ,
∴2t=10﹣t,
∴t=![]() ,
,
∴当运动时间为![]() 时,PA=QA;
时,PA=QA;
(3)存在,
∵y=![]() x2﹣
x2﹣![]() x,
x,
∴抛物线的对称轴为x=![]() ,
,
∵A(5,0),B(0,10),
∴AB=5![]()
设点M(![]() ,m),
,m),
①若BM=BA时,
∴(![]() )2+(m﹣10)2=125,
)2+(m﹣10)2=125,
∴m1=![]() ,m2=
,m2=![]() ,
,
∴M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ),
),
②若AM=AB时,
∴(![]() )2+m2=125,
)2+m2=125,
∴m3=![]() ,m4=﹣
,m4=﹣![]() ,
,
∴M3(![]() ,
,![]() ),M4(
),M4(![]() ,﹣
,﹣![]() ),
),
③若MA=MB时,
∴(![]() ﹣5)2+m2=(
﹣5)2+m2=(![]() )2+(10﹣m)2,
)2+(10﹣m)2,
∴m=5,
∴M(![]() ,5),此时点M恰好是线段AB的中点,构不成三角形,舍去,
,5),此时点M恰好是线段AB的中点,构不成三角形,舍去,
∴点M的坐标为:M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ),M4(
),M4(![]() ,﹣
,﹣![]() ),
),
“点睛”此题是二次函数综合题,主要考查了待定系数法求函数解析式,三角形的全等的性质和判定,等腰三角形的性质,解本题的关键是分情况讨论,也是本题的难点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中
中![]() ,
,![]() ,
,![]() 点P从点B出发,沿折线
点P从点B出发,沿折线![]() 运动,当它到达点A时停止,设点P运动的路程为
运动,当它到达点A时停止,设点P运动的路程为![]() 点Q是射线CA上一点,
点Q是射线CA上一点,![]() ,连接
,连接![]() 设
设![]() ,
,![]() .
.
![]() 求出
求出![]() ,
,![]() 与x的函数关系式,并注明x的取值范围;
与x的函数关系式,并注明x的取值范围;
![]() 补全表格中
补全表格中![]() 的值;
的值;
x | 1 | 2 | 3 | 4 | 6 |
| ______ | ______ | ______ | ______ | ______ |
以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点,并在x的取值范围内画出![]() 的函数图象:
的函数图象:
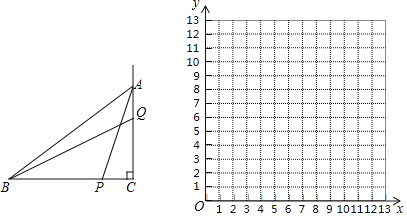
![]() 在直角坐标系内直接画出
在直角坐标系内直接画出![]() 函数图象,结合
函数图象,结合![]() 和
和![]() 的函数图象,求出当
的函数图象,求出当![]() 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬我国古代数学发展的伟大成就,某校九年级进行了一次数学知识竞赛,并设立了以我国古代数学家名字命名的四个奖项:“祖冲之奖”、“刘徽奖”、“赵爽奖”和“杨辉奖”,根据获奖情况绘制成如图1和图2所示的条形统计图和扇形统计图,并得到了获“祖冲之奖”的学生成绩统计表:
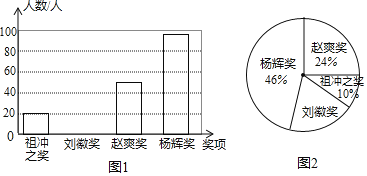
“祖冲之奖”的学生成绩统计表:
分数 | 80 | 85 | 90 | 95 |
人数 | 4 | 2 | 10 | 4 |
根据图表中的信息,解答下列问题:
![]() 这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
![]() 获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
![]() 在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“
在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“![]() ”,“
”,“![]() ”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点
”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点![]() 用列表法或树状图法求这个点在第二象限的概率.
用列表法或树状图法求这个点在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
身高分组 | 频数 | 百分比 |
x<155 | 5 | 10% |
155≤x<160 | a | 20% |
160≤x<165 | 15 | 30% |
165≤x<170 | 14 | b |
x≥170 | 6 | 12% |
总计 | 100% |
(1)填空:a=____,b=____;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
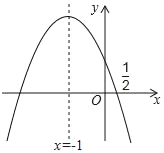
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点(![]() ,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
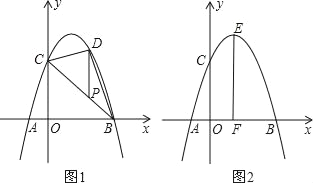
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
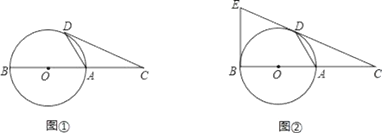
【题目】已知点C为直径BA的延长线上一点,CD切⊙O于点D,
(Ⅰ)如图①,若∠CDA=26°,求∠DAB的度数;
(Ⅱ)如图②,过点B作⊙O的切线交CD的延长线于点E,若⊙O的半径为3,BC=10,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程m x2-(m+2)x+2=0(m≠0).
(1)求证:无论m为何值时,这个方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com