
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
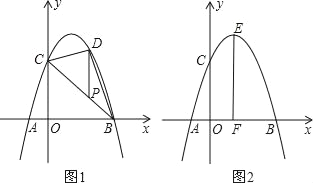
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
【答案】(1)y=﹣x2+2x+3;(2)当a=![]() 时,△BDC的面积最大,此时P(
时,△BDC的面积最大,此时P(![]() ,
, ![]() );(3)m的变化范围为:﹣
);(3)m的变化范围为:﹣![]() ≤m≤5
≤m≤5
【解析】试题分析:
解:
(1)由题意得:![]() ,解得:
,解得: ![]() ,
,
∴抛物线解析式为![]() ;
;
(2)令![]() ,
,
∴x1= -1,x2=3,即B(3,0),
设直线BC的解析式为y=kx+b′,
∴![]() ,解得:
,解得: ![]() ,
,
∴直线BC的解析式为![]() ,
,
设P(a,3-a),则D(a,-a2+2a+3),
∴PD=(-a2+2a+3)-(3-a)=-a2+3a,
∴S△BDC=S△PDC+S△PDB
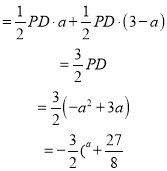 ,
,
∴当![]() 时,△BDC的面积最大,此时P(
时,△BDC的面积最大,此时P(![]() ,
, ![]() );
);
(3)由(1),y=-x2+2x+3=-(x-1)2+4,
∴OF=1,EF=4,OC=3,
过C作CH⊥EF于H点,则CH=EH=1,

当M在EF左侧时,
∵∠MNC=90°,
则△MNF∽△NCH,
∴![]() ,
,
设FN=n,则NH=3-n,
∴![]() ,
,
即n2-3n-m+1=0,
关于n的方程有解,△=(-3)2-4(-m+1)≥0,
得m≥![]() ,
,
当M在EF右侧时,Rt△CHE中,CH=EH=1,∠CEH=45°,即∠CEF=45°,
作EM⊥CE交x轴于点M,则∠FEM=45°,
∵FM=EF=4,
∴OM=5,
即N为点E时,OM=5,
∴m≤5,
综上,m的变化范围为: ![]() ≤m≤5.
≤m≤5.


科目:初中数学 来源: 题型:
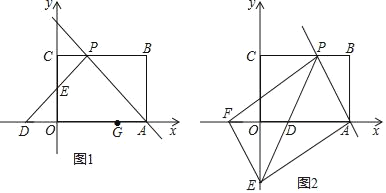
【题目】如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP和y轴上分别找一点M、N,使△GMN的周长最小,并求出此时点N的坐标和△GMN周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在数轴上有A,B两点,所表示的数分别为-10,4,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向左运动,如果设运动时间为t秒,解答下列问题:![]()
(1)运动前线段AB的长为 ; 运动1秒后线段AB的长为 ;
(2)运动t秒后,点A,点B运动的距离分别为 ;用t表示A,B分别为 .
(3)求t为何值时,点A与点B恰好重合;
(4)在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为6,若存在,求t的值; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是假命题的是( )
A. 过![]() 边形一个顶点的所有对角线,将这个多边形分成
边形一个顶点的所有对角线,将这个多边形分成![]() 个三角形
个三角形
B. 三角形中,到三个顶点距离相等的点是三条边垂直平分线的交点
C. 三角形的中线将三角形分成面积相等的两部分
D. 一组对边平行另一组对边相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了加强学生的安全意识,组织学生参加安全知识竞赛,并从中抽取了部分学生的成绩(得分均为整数,满分100分)进行统计,绘制了两幅尚不完整的统计图如图所示,
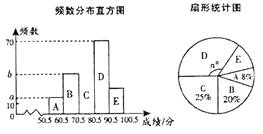
根据统计图中的信息解答下列问题:
(1)若![]() 组的频数比
组的频数比![]() 组小
组小![]() ,则频数分布直方图中
,则频数分布直方图中![]() ________,
________,![]() ________;
________;
(2)扇形统计图中![]() ________,并补全频数分布直方图;
________,并补全频数分布直方图;
(3)若成绩在![]() 分以上为优秀,全校共有
分以上为优秀,全校共有![]() 名学生,请估计成绩优秀的学生有多少名?
名学生,请估计成绩优秀的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从相距100km的A、B两地同时出发相向而行,并以各自的速度匀速行驶.甲出发2h后到达B地立即按原路返回,返回时速度提高了30km/h,回到A地后在A地休息等乙,乙在出发5h后到达A地.(友情提醒:可以借助用线段图分析题目)
(1)乙的速度是_______![]() ,甲从A地到B地的速度是_______
,甲从A地到B地的速度是_______![]() ,甲在出发_______小时到达A地.
,甲在出发_______小时到达A地.
(2)出发多长时间两人首次相遇?
(3)出发多长时间时,两人相距30千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,点E,F分别是边AD,CD上的两个动点,且满足AE+CF=BD=2,设△BEF的面积为S,则S的取值范围是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com