
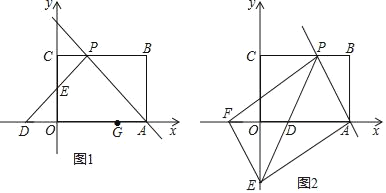
【题目】如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP和y轴上分别找一点M、N,使△GMN的周长最小,并求出此时点N的坐标和△GMN周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
【答案】(1)①y=﹣x+3,②N(0,![]() ),
),![]() ;(2) y=2x﹣2.
;(2) y=2x﹣2.
【解析】
(1)①由矩形的性质和等腰直角三角形的性质可求得∠BAP=∠BPA=45°,从而可得BP=AB=2,进而得到点P的坐标,再根据A、P两点的坐标从而可求AP的函数解析式;
②作G点关于y轴对称点G'(﹣2,0),作点G关于直线AP对称点G'(3,1),连接G'G'交y轴于N,交直线AP 于M,此时△GMN周长的最小,根据点G'、G'两点的坐标,求出其解析式,然后再根据一次函数的性质即可求解;
(2)根据矩形的性质以及已知条件求得PD=PA,进而求得DM=AM,根据平行四边形的性质得出PD=DE,然后通过得出△PDM≌△EDO得出点E和点P的坐标,即可求得.
解:(1)①∵矩形OABC,OA=3,OC=2,
∴A(3,0),C(0,2),B(3,2),
AO∥BC,AO=BC=3,∠B=90°,CO=AB=2,
∵△APD为等腰直角三角形,
∴∠PAD=45°,
∵AO∥BC,
∴∠BPA=∠PAD=45°,
∵∠B=90°,
∴∠BAP=∠BPA=45°,
∴BP=AB=2,
∴P(1,2),
设直线AP解析式y=kx+b,
∵过点A,点P,
∴![]()
∴![]() ,
,
∴直线AP解析式y=﹣x+3;
②如图所示:
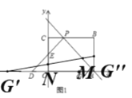
作G点关于y轴对称点G'(﹣2,0),作点G关于直线AP对称点G'(3,1)
连接G'G'交y轴于N,交直线AP 于M,此时△GMN周长的最小,
∵G'(﹣2,0),G'(3,1)
∴直线G'G'解析式y=![]() x+
x+![]()
当x=0时,y=![]() ,
,
∴N(0,![]() ),
),
∵G'G'![]() =
=![]() ,
,
∴△GMN周长的最小值为![]() ;
;
(2)如图:作PM⊥AD于M,
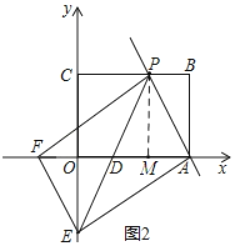
∵BC∥OA
∴∠CPD=∠PDA且∠CPD=∠APB,
∴PD=PA,且PM⊥AD,
∴DM=AM,
∵四边形PAEF是平行四边形
∴PD=DE
又∵∠PMD=∠DOE,∠ODE=∠PDM
∴△PMD≌△EOD,
∴OD=DM,OE=PM,
∴OD=DM=MA,
∵PM=2,OA=3,
∴OE=2,OM=2
∴E(0,﹣2),P(2,2)
设直线PE的解析式y=mx+n
![]()
∴![]()
∴直线PE解析式y=2x﹣2.


科目:初中数学 来源: 题型:
【题目】已知一组数![]() ,-
,-![]() ,
,![]() ,-
,-![]() ,…,
,…,![]() (从左往右数,第1个数是
(从左往右数,第1个数是![]() ,第2个数是-
,第2个数是-![]() ,第3个数是
,第3个数是![]() ,第4个数是-
,第4个数是-![]() ,依此类推,第n个数是
,依此类推,第n个数是![]() ).
).
(1)分别写出第5个、第6个数;
(2)记这组数的前n个数的和是sn,如:
s1=![]() (可表示为1+
(可表示为1+![]() );
);
s2=![]() +(-
+(-![]() )=
)=![]() (可表示为1-
(可表示为1-![]() );
);
s 3=![]() +(-
+(-![]() )+
)+![]() =
=![]() (可表示为1+
(可表示为1+![]() );
);
s4=![]() +(-
+(-![]() )+
)+![]() +(-
+(-![]() )=
)=![]() (可表示为1-
(可表示为1-![]() ).
).
请计算S99的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)3![]() +(﹣
+(﹣![]() )﹣(﹣
)﹣(﹣![]() )+2
)+2![]() .
.
(2)(﹣5)×6+(﹣125)÷(﹣5).
(3)(![]() +
+![]() )×(﹣48).
)×(﹣48).
(4)﹣12018×[(﹣2)5﹣32﹣![]() ÷(﹣
÷(﹣![]() )]﹣2.5.
)]﹣2.5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱.各种品牌的山地车相继投放市场.顺风车行经营的![]() 型车2018年6月份销售总额为
型车2018年6月份销售总额为![]() 万元,今年经过改造升级后
万元,今年经过改造升级后![]() 型车每辆销售价比去年增加
型车每辆销售价比去年增加![]() 元,若今年6月份与去年6月份卖出的
元,若今年6月份与去年6月份卖出的![]() 型车数量相同,则今年6月份
型车数量相同,则今年6月份![]() 型车销售总额将比去年6月份销售总额增加
型车销售总额将比去年6月份销售总额增加![]() .
.
(1)今年6月份![]() 型车每辆售价多少元?(用列方程的方法解答)
型车每辆售价多少元?(用列方程的方法解答)
(2)已知![]() 两种型号车今年的进货及销售价格如下表:
两种型号车今年的进货及销售价格如下表:
|
| |
进货价格(元/辆) |
|
|
销售价格(元/辆) | 今年的销售价格 |
|
该车行计划7月份进这批![]() 型车和
型车和![]() 型车共
型车共![]() 辆,且
辆,且![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车数量的两倍,应如何进货才能是这批车获利最多?
型车数量的两倍,应如何进货才能是这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=![]() ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,直线l⊥y轴于点C(C在y轴的正半轴上),与直线y=![]() 相交于点A,和双曲线y=
相交于点A,和双曲线y=![]() 交于点B,且AB=6,则点B的坐标是______.
交于点B,且AB=6,则点B的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
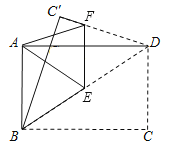
【题目】如图,将一张矩形纸片ABCD沿对角线BD折叠,点C的对应点为C′,再将所折得的图形沿EF折叠,使得点D和点A重合.若AB=3,BC=4,则折痕EF的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类。学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图。
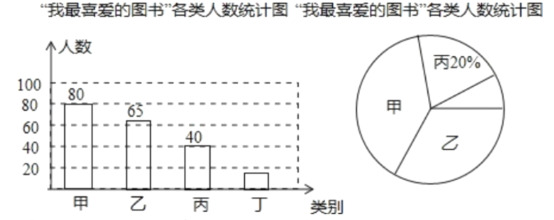
请你结合图中信息,解答下列问题:
(1)本次共调查了___名学生;
(2)被调查的学生中,最喜爱丁类图书的有___人,最喜爱甲类图书的人数占本次被调查人数的___%;
(3)在最喜爱丙类学生的图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人。
查看答案和解析>>
科目:初中数学 来源: 题型:
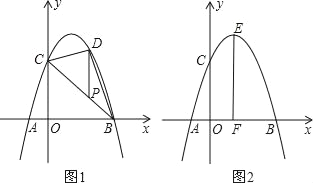
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com