
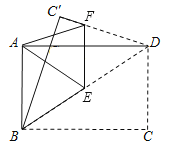
【题目】如图,将一张矩形纸片ABCD沿对角线BD折叠,点C的对应点为C′,再将所折得的图形沿EF折叠,使得点D和点A重合.若AB=3,BC=4,则折痕EF的长为__________.
【答案】![]()
【解析】分析:首先由折叠的性质与矩形的性质,证得△BND是等腰三角形,则在Rt△ABN中,利用勾股定理,借助于方程即可求得AN的长,又由△ANB≌△C′ND,易得:∠FDM=∠ABN,由三角函数的性质即可求得MF的长,又由中位线的性质求得EM的长,则问题得解.
解答: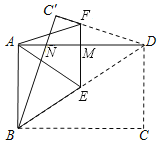 解:设BC′与AD交于N,EF与AD交于M,
解:设BC′与AD交于N,EF与AD交于M,
根据折叠的性质可得:∠NBD=∠CBD,AM=DM=1/2AD,∠FMD=∠EMD=90°,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=4,∠BAD=90°,
∴∠ADB=∠CBD,
∴∠NBD=∠ADB,
∴BN=DN,
设AN=x,则BN=DN=4-x,
∵在Rt△ABN中,AB2+AN2=BN2,
∴32+x2=(4-x)2,
∴x=7/8,
即AN=7/8,
∵C′D=CD=AB=3,∠BAD=∠C′=90°,∠ANB=∠C′ND,
∴△ANB≌△C′ND(AAS),
∴∠FDM=∠ABN,
∴tan∠FDM=tan∠ABN,
∴AN/AB=MF/MD,
∴7/(8/3)=MF/2,
∴MF=7/12,
由折叠的性质可得:EF⊥AD,
∴EF∥AB,
∵AM=DM,
∴ME=1/2AB=3/2,
∴EF=ME+MF=3/2+7/12=25/12.


科目:初中数学 来源: 题型:
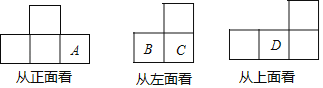
【题目】一个几何体由大小相同的小立方体搭成,从三个方向看到的几何体的形状图如图所示.
(1)求A,B,C,D这4个方格位置上的小立方体的个数;
(2)这个几何体是由多少块小立方体组成的?
查看答案和解析>>
科目:初中数学 来源: 题型:
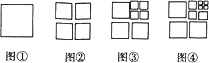
【题目】将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形…,如此下去,则第2014个图中共有正方形的个数为( )
A. 2014. B. 2017 C. 6040 D. 6044
查看答案和解析>>
科目:初中数学 来源: 题型:
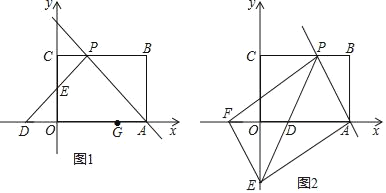
【题目】如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP和y轴上分别找一点M、N,使△GMN的周长最小,并求出此时点N的坐标和△GMN周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅在铺瓷砖时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图①.然后,他用这8块瓷砖又拼出一个正方形,如图②,中间恰好空出一个边长为1的小正方形(阴影部分).
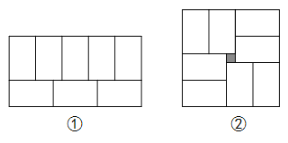
(1)请你根据图①写出小长方形的长与宽之比为 ;
(2)请你根据图②列出方程,求出小长方形的长与宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①若![]() 则
则![]() 为负数;②若关于的方程
为负数;②若关于的方程![]() 有无数解,则a=b;③若
有无数解,则a=b;③若![]() ,则关于
,则关于![]() 的方程
的方程![]() 的解为
的解为![]() ;④若
;④若![]() 则
则![]() ;⑥若
;⑥若![]() ,且
,且![]() ,则
,则![]() 一定是为程
一定是为程![]() 的解;其中结论正确个数有( )
的解;其中结论正确个数有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宇航员翟志刚在太空进行了19分35秒的舱外活动中,飞行了9 165 000 米,成为中国“飞得最高、走得最快”的人.将9 165 000 米保留两位有效数字用科学记数法记为( )米
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了加强学生的安全意识,组织学生参加安全知识竞赛,并从中抽取了部分学生的成绩(得分均为整数,满分100分)进行统计,绘制了两幅尚不完整的统计图如图所示,
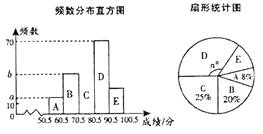
根据统计图中的信息解答下列问题:
(1)若![]() 组的频数比
组的频数比![]() 组小
组小![]() ,则频数分布直方图中
,则频数分布直方图中![]() ________,
________,![]() ________;
________;
(2)扇形统计图中![]() ________,并补全频数分布直方图;
________,并补全频数分布直方图;
(3)若成绩在![]() 分以上为优秀,全校共有
分以上为优秀,全校共有![]() 名学生,请估计成绩优秀的学生有多少名?
名学生,请估计成绩优秀的学生有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com