
【题目】为了弘扬我国古代数学发展的伟大成就,某校九年级进行了一次数学知识竞赛,并设立了以我国古代数学家名字命名的四个奖项:“祖冲之奖”、“刘徽奖”、“赵爽奖”和“杨辉奖”,根据获奖情况绘制成如图1和图2所示的条形统计图和扇形统计图,并得到了获“祖冲之奖”的学生成绩统计表:
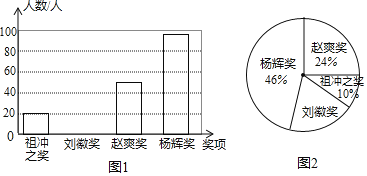
“祖冲之奖”的学生成绩统计表:
分数 | 80 | 85 | 90 | 95 |
人数 | 4 | 2 | 10 | 4 |
根据图表中的信息,解答下列问题:
![]() 这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
![]() 获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
![]() 在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“
在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“![]() ”,“
”,“![]() ”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点
”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点![]() 用列表法或树状图法求这个点在第二象限的概率.
用列表法或树状图法求这个点在第二象限的概率.
【答案】(1)刘徽奖的人数为![]() 人,补全统计图见解析;(2)获得“祖冲之奖”的学生成绩的中位数是90分,众数是90分;(3)
人,补全统计图见解析;(2)获得“祖冲之奖”的学生成绩的中位数是90分,众数是90分;(3)![]() (点在第二象限)
(点在第二象限)![]() .
.
【解析】
(1)先根据祖冲之奖的人数及其百分比求得总人数,再根据扇形图求出赵爽奖、杨辉奖的人数,继而根据各奖项的人数之和等于总人数求得刘徽奖的人数,据此可得;
(2)根据中位数和众数的定义求解可得;
(3)列表得出所有等可能结果,再找到这个点在第二象限的结果,根据概率公式求解可得.
(1)∵获奖的学生人数为20÷10%=200人,∴赵爽奖的人数为200×24%=48人,杨辉奖的人数为200×46%=92人,则刘徽奖的人数为200﹣(20+48+92)=40,补全统计图如下:
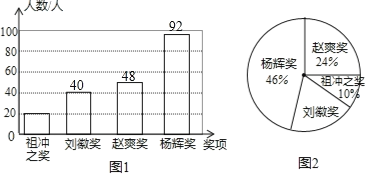
故答案为:40;
(2)获得“祖冲之奖”的学生成绩的中位数是90分,众数是90分.
故答案为:90、90;
(3)列表法:
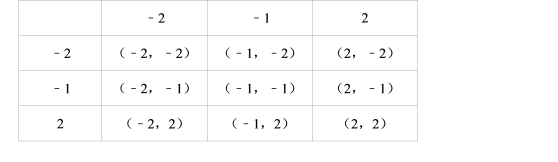
∵第二象限的点有(﹣2,2)和(﹣1,2),∴P(点在第二象限)![]() .
.


科目:初中数学 来源: 题型:
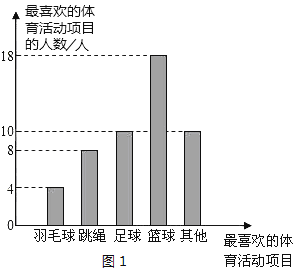
【题目】某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据,如图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢足球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有400名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢篮球活动的人数约为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
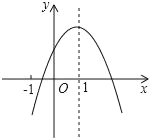
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列6个结论:
①abc<0;
②b<a﹣c;
③4a+2b+c>0;
④2c<3b;
⑤a+b<m(am+b),(m≠1的实数)
⑥2a+b+c>0,其中正确的结论的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )

A. 6→3 B. 7→16 C. 7→8 D. 6→15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂生产一种半成品食材,产量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足函数关系式
满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材的市场需求量
,从市场反馈的信息发现,该半成品食材的市场需求量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足一次函数关系,如下表:
满足一次函数关系,如下表:
销售价格 | 2 | 4 |
| 10 |
市场需求量 | 12 | 10 |
| 4 |
已知按物价部门规定销售价格x不低于2元![]() 千克且不高于10元
千克且不高于10元![]() 千克
千克
![]() 求q与x的函数关系式;
求q与x的函数关系式;
![]() 当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
![]() 当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃
当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃![]() 若该半成品食材的成本是2元
若该半成品食材的成本是2元![]() 千克.
千克.
![]() 求厂家获得的利润
求厂家获得的利润![]() 百元
百元![]() 与销售价格x的函数关系式;
与销售价格x的函数关系式;
![]() 当厂家获得的利润
当厂家获得的利润![]() 百元
百元![]() 随销售价格x的上涨而增加时,直接写出x的取值范围
随销售价格x的上涨而增加时,直接写出x的取值范围![]() 利润
利润![]() 售价
售价![]() 成本
成本![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABO中,∠B=90°,∠OAB=30°,OA=3.以点O为原点,斜边OA所在直线为x轴,建立平面直角坐标系,以点P(4,0)为圆心,PA长为半径画圆,⊙P与x轴的另一交点为N,点M在⊙P上,且满足∠MPN=60°.⊙P以每秒1个单位长度的速度沿x轴向左运动,设运动时间为ts,解答下列问题:
(发现)(1)![]() 的长度为多少;
的长度为多少;
(2)当t=2s时,求扇形MPN(阴影部分)与Rt△ABO重叠部分的面积.
(探究)当⊙P和△ABO的边所在的直线相切时,求点P的坐标.
(拓展)当![]() 与Rt△ABO的边有两个交点时,请你直接写出t的取值范围.
与Rt△ABO的边有两个交点时,请你直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济水平的不断提升,越来越多的人选择到电影院去观看电影,体验视觉盛宴,并且更多的人通过淘票票,猫眼等网上平台购票,快捷且享受更多优惠,电影票价格也越来越便宜.2018年从网上平台购买5张电影票的费用比在现场购买3张电影票的费用少10元,从网上平台购买4张电影票的费用和现场购买2张电影票的费用共为190元.
(1)请问2018年在网上平台购票和现场购票的每张电影票的价格各为多少元?
(2)2019年“元旦”当天,南坪上海城的“华谊兄弟影院”按照2018年在网上平台购票和现场购票的电影票的价格进行销售,当天网上和现场售出电影票总票数为600张.“元旦”假期刚过,观影人数出现下降,于是该影院决定将1月2日的现场购票的价格下调,网上购票价格保持不变,结果发现现场购票每张电影票的价格每降价0.5元,则当天总票数比“元旦”当天总票数增加4张,经统计,1月2日的总票数中有![]() 通过网上平台售出,其余均由电影院现场售出,且当天票房总收益为19800元,请问该电影院在1月2日当天现场购票每张电影票的价格下调了多少元?
通过网上平台售出,其余均由电影院现场售出,且当天票房总收益为19800元,请问该电影院在1月2日当天现场购票每张电影票的价格下调了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
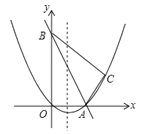
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
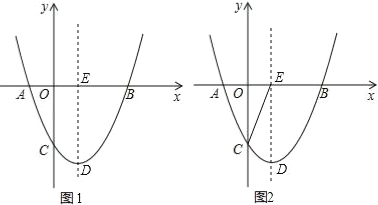
【题目】如图1,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣2),顶点为D,对称轴交x轴于点E.
(1)求该二次函数的解析式;
(2)设M为该抛物线对称轴左侧上的一点,过点M作直线MN∥x轴,交该抛物线于另一点N.是否存在点M,使四边形DMEN是菱形?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)连接CE(如图2),设点P是位于对称轴右侧该抛物线上一点,过点P作PQ⊥x轴,垂足为Q.连接PE,请求出当△PQE与△COE相似时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com