
【题目】如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.

(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留π和根号).
【答案】解:(1)证明:连接OD,
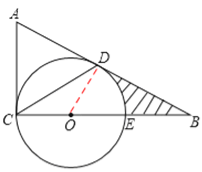
∵AB是⊙O切线,∴∠ODB=90°。
∴BE=OE=OD=2。
∴∠B=30°,∠DOB=60°。
∵OD=OC,∴∠DCB=∠ODC=![]() ∠DOB=30°。
∠DOB=30°。
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°。∴∠A=2∠DCB。
(2)∵∠ODB=90°,OD=2,BO=2+2=4,由勾股定理得:BD=2![]() ,
,
∴阴影部分的面积![]()
【解析】
试题(1)连接OD,求出∠ODB=90°,求出∠B=30°,∠DOB=60°,求出∠DCB度数,关键三角形内角和定理求出∠A,即可得出答案。
(2)根据勾股定理求出BD,分别求出△ODB和扇形DOE的度数,即可得出答案。


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边AD绕点A顺时针旋转角度m(0°<m<360°),得到线段AP,连接PB,PC.当△BPC是等腰三角形时,m的值为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
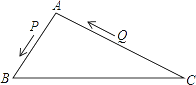
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:①△BMD≌△DFE;②△NBE∽△DBC;③AC=2DF;④EFAB=CFBC,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积.
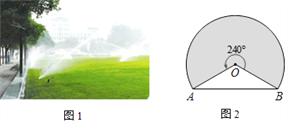
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在![]() 上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是_____.
上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
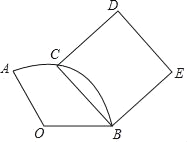
【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P(如图2),则六边形AEFCHG面积的最大值是( )

A. ![]() B.
B. ![]() C. 2﹣
C. 2﹣ ![]() D. 1+
D. 1+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
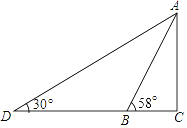
【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com