
【题目】随着信息技术的迅猛发展,人们购物的支付方式更加多样、便捷,为调查大学生购物支付方式,某大学一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
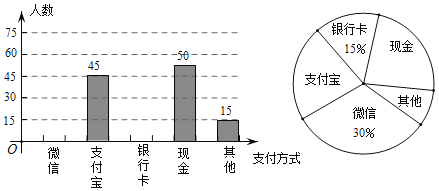
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为
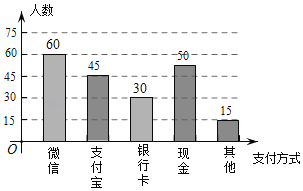
(2)将条形统计图补充完整;
(3)若该大学有10000名学生,请你估计购物选择用支付宝支付方式的学生约有多少人?
【答案】(1)200,81°;(2)补充完整的条形统计图如图所示;见解析;(3)购物选择用支付宝支付方式的学生约有2250人.
【解析】
(1)根据支付宝、现金、其他的人数和所占的百分比可以求得本次调查的人数,并求出示“支付宝”支付的扇形圆心角的度数;
(2)根据(1)中的结果可以求得使用微信和银行卡的人数,从而可以将条形统计图补充完整;
(3)根据统计图中的数据可以求得购物选择用支付宝支付方式的学生约有多少人.
(1)本次调查的人数为:(45+50+15)÷(1﹣15%﹣30%)=200,
表示“支付宝”支付的扇形圆心角的度数为:360°×![]() =81°,
=81°,
故答案为:200,81°;
(2)使用微信的人数为:200×30%=60,使用银行卡的人数为:200×15%=30,
补充完整的条形统计图如图所示;
(3)10000×![]() =2250(人),
=2250(人),
答:购物选择用支付宝支付方式的学生约有2250人.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BC边在x轴正半轴上,中线BD的反向延长线交y轴负半轴于点E.双曲线y=![]() 一条分支经过点A,若S△BEC=4,则k等于( )
一条分支经过点A,若S△BEC=4,则k等于( )
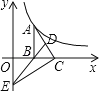
A. 4B. 8C. 12D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
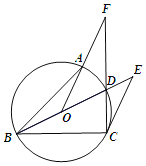
【题目】已知,如图,BD为⊙O的直径,点A、C在⊙O上并位于BD的两侧,∠ABC=45°,连结CD、OA并延长交于点F,过点C作⊙O的切线交BD延长线于点E.
(1)求证:∠F=∠ECF;
(2)当DF=6,tan∠EBC=![]() ,求AF的值.
,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,且满足BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作FG的平行线,交DA的延长线于点N,连接NG.

求证:BE=2CF;
试猜想四边形BFGN是什么特殊的四边形,并对你的猜想加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、E在⊙O上,∠B=2∠ACE,在BA的延长线上有一点P,使得∠P=∠BAC,弦CE交AB于点F,连接AE.
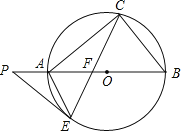
(1)求证:PE是⊙O的切线;
(2)若AF=2,AE=EF=![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知开口向下的抛物线y=ax2﹣2ax+3与x轴的交点为A、B两点(点A在点B的左边),与y轴的交点为C,OC=3OA
(1)请直接写出该抛物线解析式;
(2)如图,D为抛物线的顶点,连接BD、BC,P为对称轴右侧抛物线上一点.若∠ABD=∠BCP,求点P的坐标
(3)在(2)的条件下,M、N是抛物线上的动点.若∠MPN=90°,直线MN必过一定点,请求出该定点的坐标.
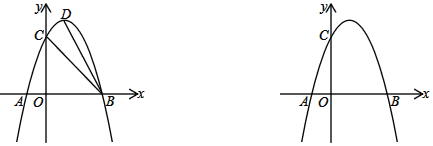
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发一种新的药物,据监测,如果成年人按规定的剂量服用,服药后2小时,每毫升血液中的含药量达到最大值,之后每毫升血液中的含药量逐渐衰减.若一次服药后每毫升血液中的含药量y(单位:微克)与服药后的时间t(单位:小时)之间近似满足某种函数关系,下表是y与t的几组对应值,其部分图象如图所示.
t | 0 | 1 | 2 | 3 | 4 | 6 | 8 | 10 | … |
y | 0 | 2 | 4 | 2.83 | 2 | 1 | 0.5 | 0.25 | … |
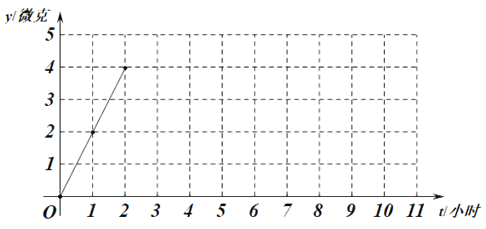
(1)在所给平面直角坐标系中,继续描出上表中已列出数值所对应的点(t,y),并补全该函数的图象;
(2)结合函数图象,解决下列问题:
①某病人第一次服药后5小时,每毫升血液中的含药量约为_______微克;若每毫升血液中含药量不少于0.5微克时治疗疾病有效,则第一次服药后治疗该疾病有效的时间共持续约_______小时;
②若某病人第一次服药后8小时进行第二次服药,第二次服药对血液中含药量的影响与第一次服药相同,则第二次服药后2小时,每毫升血液中的含药量约为_______微克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,∠ABC的平分线BF交AD于点F,交BC于点D.
(1)求证:BE=EF;
(2)若DE=4,DF=3,求AF的长.
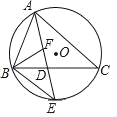
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com