
【题目】已知开口向下的抛物线y=ax2﹣2ax+3与x轴的交点为A、B两点(点A在点B的左边),与y轴的交点为C,OC=3OA
(1)请直接写出该抛物线解析式;
(2)如图,D为抛物线的顶点,连接BD、BC,P为对称轴右侧抛物线上一点.若∠ABD=∠BCP,求点P的坐标
(3)在(2)的条件下,M、N是抛物线上的动点.若∠MPN=90°,直线MN必过一定点,请求出该定点的坐标.
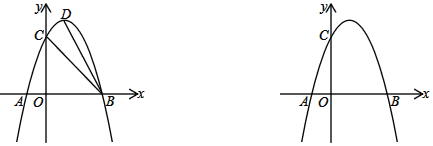
【答案】(1)y=﹣x2+2x+3;(2)点P坐标为(![]() ,
,![]() )(3)直线MN过定点(
)(3)直线MN过定点(![]() ,
,![]() ).
).
【解析】
(1)求出点A坐标,代入y=ax2﹣2ax+3求出a的值即可求出该抛物线解析式;
(2)分两种情况讨论:若点P在抛物线对称轴右侧且在x轴上方,若点P在x轴下方;
(3)过P作PH∥y轴,分别过点M、N作MG⊥PH于G,NH⊥PH于H.先证明△MPG∽△PNH,根据相似比列出关于k的方程,求得k的两个值,从而用n的代数式表示直线MN的方程,得出直线MN必过一定点.
(1)当x=0时,y=ax2﹣2ax+3=3,
∴C(0,3),OC=3OA=3,
∴OA=1,A(﹣1,0),
把点A(﹣1,0)代入抛物线解析式得:a+2a+3=0,
解得:a=﹣1,
∴抛物线解析式为y=﹣x2+2x+3;
(2)如图1,若点P在抛物线对称轴右侧且在x轴上方,
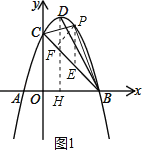
过点P作PE∥y轴交BC于点E,PF⊥BC于点F,过点D作DH⊥x轴于点H,
∴∠CFP=∠BHD=90°,
∵当y=﹣x2+2x+3=0时,解得:x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D(1,4),
∴DH=4,BH=3﹣1=2,
∴BD=![]() ,
,
∴Rt△BDH中,sin∠ABD=![]() ,
,
∵C(0,3)
∴BC=![]() ,PC=
,PC=![]() ,
,
设直线BC解析式为y=kx+b,
∴![]() ,解得:
,解得:![]() ,
,
∴直线BC解析式为y=﹣x+3,
设P(p,﹣p2+2p+3)(1<p<3),则E(p,﹣p+3),
∴PE=﹣p2+2p+3﹣(﹣p+3)=﹣p2+3p,
∵S△BCP=![]() PEOB=
PEOB=![]()
![]() BCPF,
BCPF,
∴PF=![]() ,
,
∵∠ABD=∠BCP,
∴Rt△CPF中,sin∠BCP=![]() =sin∠ABD=
=sin∠ABD=![]() ,
,
∴PF=![]() PC,
PC,
∴PF2=![]() PC2,
PC2,
解得:p1=﹣1(舍去),p2=![]() ,
,
∴﹣p2+2p+3=![]() ,
,
∴点P坐标为(![]() ,
,![]() )
)
如图2,若点P在x轴下方,
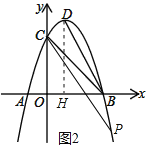
∵tan∠ABD=![]() =2>tan45°,
=2>tan45°,
∴∠ABD>45°,
∵∠BCP<∠BOC即∠BCP<45°,
∴∠ABD与∠BCP不可能相等.
综上所述,点P坐标为(![]() ,
,![]() );
);
(3)如图3,过P作PH∥y轴,分别过点M、N作MG⊥PH于G,NH⊥PH于H.
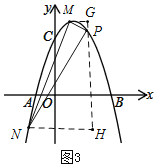
设直线MN的解析式为y=kx+n,M(x1,y1)、N(x2,y3),
令kx+n=﹣x2+2x+3,即=x2+(k﹣2)x+n﹣3=0,
∴x1+x2=2﹣k,x1x2=n﹣3,
∴y1+y2=k(x1+x2)+2n=k(2﹣k)+2n,
y1y2=(kx1+n)(kx2+n)=k2x1x2+nk(x1+x2)+n2=﹣3k2+2nk+n2,
∵∠G=∠MPN=∠H,
∴△MPG∽△PNH,
∴![]() ,
,
∵P坐标为(![]() ,
,![]() ),
),
MG=![]() ﹣x1,PH=y1﹣
﹣x1,PH=y1﹣![]() ,HN=
,HN=![]() ,GP=
,GP=![]() ,
,
∴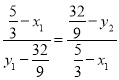 ,
,
整理,得![]() ,
,
∴![]() ,
,
解得 k1=﹣3n+![]() ,k2=
,k2=![]() ,
,
∴直线MN;y=(﹣3n+![]() )x+n=(﹣3x+1)n+
)x+n=(﹣3x+1)n+![]() ,过定点(
,过定点(![]() ,
,![]() );
);
或y=(![]() )x+n=(
)x+n=(![]() )n+
)n+![]() ,过定点(
,过定点(![]() ,
,![]() )即P点,舍去.
)即P点,舍去.
∴直线MN过定点(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】在直线l上摆放着三个正方形
(1)如图1,已知水平放置的两个正方形的边长依次是a,b斜着放置的正方形的面积S= ,两个直角三角形的面积和为 ;(均用a,b表示)
(2)如图2,小正方形面积S1=1,斜着放置的正方形的面积S=4,求图中两个钝角三角形的面积m1和m2,并给出图中四个三角形的面积关系;
(3)图3是由五个正方形所搭成的平面图,T与S分别表示所在的三角形与正方形的面积,试写出T与S的关系式,并利用(1)和(2)的结论说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
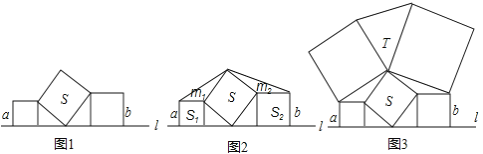
【题目】某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
![]()
成绩x/分 | 频数 | 频率 | |
第1段 | x<60 | 2 | 0.04 |
第2段 | 60≤x<70 | 6 | 0.12 |
第3段 | 70≤x<80 | 9 | b |
第4段 | 80≤x<90 | a | 0.36 |
第5段 | 90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)样本中,部分学生成绩的中位数落在第_______段;
(4)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市农林种植专家指导贫困户种植红梨和青枣,收获的红梨和青枣优先进入该市水果市场.已知某水果经销商购进了红梨和青枣两种水果各10箱,分配给下属的甲、乙两个零售店(分别简称甲店、乙店)销售.预计每箱水果的盈利情况如表
红梨/箱 | 青枣/箱 | |
甲店 | 22元 | 34元 |
乙店 | 18元 | 26元 |
(1)若甲、乙两店各配货10箱,其中甲店配红梨2箱,青枣8箱;乙店配红梨8箱,青枣2箱,请你计算出经销商能盈利多少元?
(2)若甲、乙两店各配货10箱,且在保证乙店盈利不小于200元的条件下,请你设计出使水果经销商盈利最大的配货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
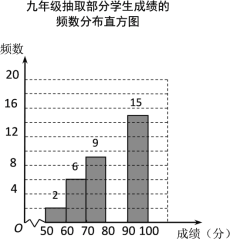
【题目】随着信息技术的迅猛发展,人们购物的支付方式更加多样、便捷,为调查大学生购物支付方式,某大学一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为
(2)将条形统计图补充完整;
(3)若该大学有10000名学生,请你估计购物选择用支付宝支付方式的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作平行四边形一边中点”的尺规作图过程.
已知:平行四边形ABCD.
求作:点M,使点M为边AD的中点.

作法:如图,
①作射线BA;
②以点A为圆心,CD长为半径画弧,交BA的延长线于点E;
③连接EC交AD于点M.
所以点M就是所求作的点.
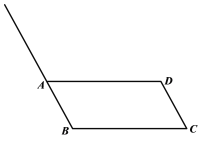
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接AC,ED.
∵四边形ABCD是平行四边形,
∴![]() .
.
∵AE= ,
∴四边形EACD是平行四边形( )(填推理的依据).
∴![]() ( )(填推理的依据).
( )(填推理的依据).
∴点M为所求作的边AD的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)的对称轴为x=-1,与x轴的一个交点为(2,0).若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
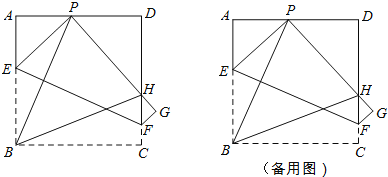
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com