
【题目】某市农林种植专家指导贫困户种植红梨和青枣,收获的红梨和青枣优先进入该市水果市场.已知某水果经销商购进了红梨和青枣两种水果各10箱,分配给下属的甲、乙两个零售店(分别简称甲店、乙店)销售.预计每箱水果的盈利情况如表
红梨/箱 | 青枣/箱 | |
甲店 | 22元 | 34元 |
乙店 | 18元 | 26元 |
(1)若甲、乙两店各配货10箱,其中甲店配红梨2箱,青枣8箱;乙店配红梨8箱,青枣2箱,请你计算出经销商能盈利多少元?
(2)若甲、乙两店各配货10箱,且在保证乙店盈利不小于200元的条件下,请你设计出使水果经销商盈利最大的配货方案.
【答案】(1)经销商能盈利512元;(2)盈利最大的配货方案是甲店配红梨3箱,青枣7箱;乙店配红梨7箱,青枣3箱,最大盈利金额是508元.
【解析】
(1)经销商能盈利=水果箱数×每箱水果的盈利;
(2)根据题意得出红梨乙店盈利×(10x)+青枣乙店盈利×x不小于200元,列出不等式,求出不等式的解集,再由经销商盈利y=红梨甲店盈利×x+青枣甲店盈利×(10x)+红梨乙店盈利×(10x)+青枣甲店盈利×x,得到 y与x的函数关系式,最后根据函数性质求得最大盈利时x的值,便可得出结果.
(1)22×2+18×8+34×8+26×2=512(元),
所以经销商能盈利512元.
(2)设甲店配红梨x箱,则甲店配青枣(10﹣x)箱,乙店配红梨(10﹣x)箱,乙店配青枣10﹣(10﹣x)=x箱
因为18×(10﹣x)+26x≥200,所以x≥![]() .
.
经销商盈利为y=22x+34×(10﹣x)+18×(10﹣x)+26x=﹣4x+520.
当x=3时,y值最大,
盈利最大的配货方案是甲店配红梨3箱,青枣7箱;乙店配红梨7箱,青枣3箱.
最大盈利金额是﹣4×3+520=508(元).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:

请你根据统计图回答下列问题:
(1)喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;
(2)请你估计全校500名学生中最喜欢“排球”项目的有多少名?
(3)在扇形统计图中,“篮球”部分所对应的圆心角是多少度?
(4)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y=![]() 在第一象限图象上一点,连接OA,过点A作AB∥x轴(点B在点A右侧),连接OB,若OB平分∠AOX,且点B的坐标是(8,4),则k的值是( )
在第一象限图象上一点,连接OA,过点A作AB∥x轴(点B在点A右侧),连接OB,若OB平分∠AOX,且点B的坐标是(8,4),则k的值是( )

A.6B.8C.12D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)试求抛物线的解析式;
(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=![]() ,试求m的最大值及此时点P的坐标;
,试求m的最大值及此时点P的坐标;
(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,且满足BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作FG的平行线,交DA的延长线于点N,连接NG.

求证:BE=2CF;
试猜想四边形BFGN是什么特殊的四边形,并对你的猜想加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
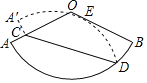
【题目】如图,已知扇形AOB的圆心角为120°,点C是半径OA上一点,点D是![]() 上一点.将扇形AOB沿CD对折,使得折叠后的图形恰好与半径OB相切于点E.若∠OCD=45°,OC=
上一点.将扇形AOB沿CD对折,使得折叠后的图形恰好与半径OB相切于点E.若∠OCD=45°,OC=![]() +1,则扇形AOB的半径长是( )
+1,则扇形AOB的半径长是( )
A. 2+![]() B. 2+
B. 2+![]() C. 2
C. 2![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知开口向下的抛物线y=ax2﹣2ax+3与x轴的交点为A、B两点(点A在点B的左边),与y轴的交点为C,OC=3OA
(1)请直接写出该抛物线解析式;
(2)如图,D为抛物线的顶点,连接BD、BC,P为对称轴右侧抛物线上一点.若∠ABD=∠BCP,求点P的坐标
(3)在(2)的条件下,M、N是抛物线上的动点.若∠MPN=90°,直线MN必过一定点,请求出该定点的坐标.
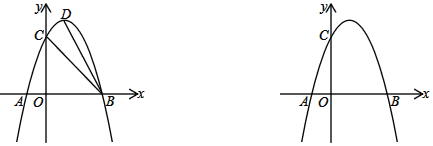
查看答案和解析>>
科目:初中数学 来源: 题型:
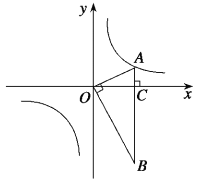
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图像上.
的图像上.
(1)k= ;
(2)在x轴的负半轴上存在一点 P ,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE,直接写出点E的坐标,并判断点E是否在该反比例函数的图像上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
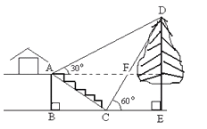
【题目】某校在苏州园林研学时,校综合实践活动小组的同学欲测量公园内一棵树![]() 的高度,他们在这棵树的正前方一座楼亭前的台阶上
的高度,他们在这棵树的正前方一座楼亭前的台阶上![]() 点处测得树顶端
点处测得树顶端![]() 的仰角为
的仰角为![]() ,朝着这棵树的方向走到台阶下的点
,朝着这棵树的方向走到台阶下的点![]() 处,测得树顶端
处,测得树顶端![]() 的仰角为
的仰角为![]() .已知
.已知![]() 点的高度
点的高度![]() 为
为![]() 米,台阶
米,台阶![]() 的坡度为
的坡度为![]() (即
(即![]() ),且
),且![]() 三点在同一条直线上.请根据以上条件求出树
三点在同一条直线上.请根据以上条件求出树![]() 的高度(侧倾器的高度忽略不计).
的高度(侧倾器的高度忽略不计).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com