
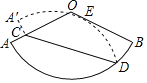
【题目】如图,已知扇形AOB的圆心角为120°,点C是半径OA上一点,点D是![]() 上一点.将扇形AOB沿CD对折,使得折叠后的图形恰好与半径OB相切于点E.若∠OCD=45°,OC=
上一点.将扇形AOB沿CD对折,使得折叠后的图形恰好与半径OB相切于点E.若∠OCD=45°,OC=![]() +1,则扇形AOB的半径长是( )
+1,则扇形AOB的半径长是( )
A. 2+![]() B. 2+
B. 2+![]() C. 2
C. 2![]() D.
D. ![]()
【答案】B
【解析】
作O关于CD的对称点F,连接CF、EF,则EF为扇形AOB的半径,由折叠的性质得:∠FCD=∠OCD=45°,FC=OC=![]() +1,得出△OCF是等腰直角三角形,得出∠COF=45°,OF=
+1,得出△OCF是等腰直角三角形,得出∠COF=45°,OF=![]() OC=
OC=![]() +
+![]() ,∠EOF=∠AOB﹣∠COF=75°,由切线的性质得出∠OEF=90°,得出∠OFE=15°,由三角函数即可得出结果.
,∠EOF=∠AOB﹣∠COF=75°,由切线的性质得出∠OEF=90°,得出∠OFE=15°,由三角函数即可得出结果.
作O关于CD的对称点F,连接CF、EF,如图1所示:
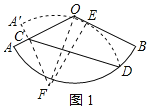
则EF为扇形AOB的半径,
由折叠的性质得:∠FCD=∠OCD=45°,FC=OC=![]() +1,
+1,
∴∠OCF=90°,
∴△OCF是等腰直角三角形,
∴∠COF=45°,OF=![]() OC=
OC=![]() +
+![]() ,
,
∴∠EOF=∠AOB﹣∠COF=75°,
∵折叠后的图形恰好与半径OB相切于点E,
∴∠OEF=90°,
∴∠OFE=15°,
∵cos∠OFE=![]() cos15°=
cos15°=![]() ,
,
如图2所示:
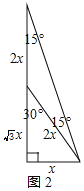
∴EF=OF×cos15°=(![]() +
+![]() )×
)×![]() =2+
=2+![]() ;
;
故选:B.


科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
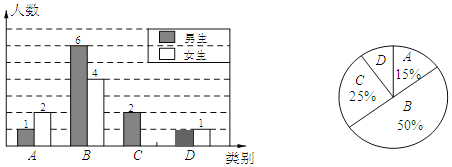
【题目】李老师为了解某校学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.绘制成如下统计图.
(1)李老师一共调查了多少名同学?并将下面条形统计图补充完整.
(2)若该校有1000名学生,则数学课前预习“很好”和“较好”总共约多少人?
(3)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,求出所选两位同学恰好是一位男同学和一位女同学的概率.(要求列表或树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
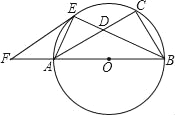
【题目】如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市农林种植专家指导贫困户种植红梨和青枣,收获的红梨和青枣优先进入该市水果市场.已知某水果经销商购进了红梨和青枣两种水果各10箱,分配给下属的甲、乙两个零售店(分别简称甲店、乙店)销售.预计每箱水果的盈利情况如表
红梨/箱 | 青枣/箱 | |
甲店 | 22元 | 34元 |
乙店 | 18元 | 26元 |
(1)若甲、乙两店各配货10箱,其中甲店配红梨2箱,青枣8箱;乙店配红梨8箱,青枣2箱,请你计算出经销商能盈利多少元?
(2)若甲、乙两店各配货10箱,且在保证乙店盈利不小于200元的条件下,请你设计出使水果经销商盈利最大的配货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果零售商店,通过对市场行情的调查,了解到两种水果销路比较好,一种是冰糖橙,一种是睡美人西瓜.通过两次订货购进情况分析发现,买40箱冰糖橙和15箱睡美人西瓜花去2000元,买20箱冰糖橙和30箱睡美人西瓜花去1900元.
(1)请求出购进这两种水果每箱的价格是多少元?
(2)该水果零售商在五一期间共购进了这两种水果200箱,冰糖橙每箱以40元价格出售,西瓜以每箱50元的价格出售,获得的利润为w元.设购进的冰糖橙箱数为a箱,求w关于a的函数关系式;
(3)在条件(2)的销售情况下,但是每种水果进货箱数不少于30箱,西瓜的箱数不少于冰糖橙箱数的5倍,请你设计进货方案,并计算出该水果零售商店能获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
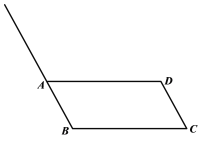
【题目】下面是小东设计的“作平行四边形一边中点”的尺规作图过程.
已知:平行四边形ABCD.
求作:点M,使点M为边AD的中点.

作法:如图,
①作射线BA;
②以点A为圆心,CD长为半径画弧,交BA的延长线于点E;
③连接EC交AD于点M.
所以点M就是所求作的点.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接AC,ED.
∵四边形ABCD是平行四边形,
∴![]() .
.
∵AE= ,
∴四边形EACD是平行四边形( )(填推理的依据).
∴![]() ( )(填推理的依据).
( )(填推理的依据).
∴点M为所求作的边AD的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
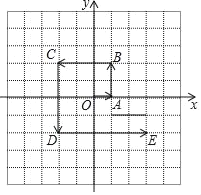
【题目】每个小方格都是边长为1的正方形,在平面直角坐标系中.
(1)写出图中从原点O出发,按箭头所指方向先后经过的A、B、C、D、E这几个点点的坐标;
(2)按图中所示规律,找到下一个点F的位置并写出它的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E为矩形ABCD边AD上一点,点P点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为y cm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分).则下列结论:①AD=BE=5cm;②当0<t≤5时,![]() ;③直线NH的解析式为y=
;③直线NH的解析式为y=![]() t+27; ④若△ABE与△QBP相似,则t=
t+27; ④若△ABE与△QBP相似,则t=![]() 秒, 其中正确结论的个数为( )
秒, 其中正确结论的个数为( )


A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com