
����Ŀ��ijˮ�������̵꣬ͨ�����г�����ĵ��飬�˽����ˮ����·�ȽϺã�һ���DZ��dzȣ�һ����˯�������ϣ�ͨ�����ζ�����������������֣���40����dzȺ�15��˯�������ϻ�ȥ2000Ԫ����20����dzȺ�30��˯�������ϻ�ȥ1900Ԫ��
��1�����������������ˮ��ÿ��ļ۸��Ƕ���Ԫ��
��2����ˮ������������һ�ڼ乲������������ˮ��200�䣬���dz�ÿ����40Ԫ�۸���ۣ�������ÿ��50Ԫ�ļ۸���ۣ���õ�����ΪwԪ���蹺���ı��dz�����Ϊa�䣬��w����a�ĺ�����ϵʽ��
��3����������2������������£�����ÿ��ˮ����������������30�䣬���ϵ����������ڱ��dz�������5����������ƽ������������������ˮ�������̵��ܻ�õ���������Ƕ��٣�
���𰸡���1��ÿ����dzȽ���Ϊ35Ԫ��ÿ��˯�������Ͻ���Ϊ40Ԫ����2��w����5a+2000����3����������dz�30�䣬����˯��������170���ˮ�������̵��ܻ�õ���������������Ϊ1850Ԫ��
��������
��1����ÿ����dz�xԪ��ÿ��˯��������yԪ����������40����dzȺ�15��˯�������ϻ�ȥ2000Ԫ����20����dzȺ�30��˯�������ϻ�ȥ1900Ԫ���г������鲢���
��2�����ݣ�1���Ľ����Լ��������ۼ۩��ɱ�����ɣ�
��3���蹺����dz�a�䣬����˯��������Ϊ��200��a���䣬������ÿ��ˮ����������������30�䣬���ϵ����������ڱ��dz�������5�����г�����ʽ�����a��ȡֵ��Χ���ٸ���һ�κ��������ʽ�ɣ�
��1����ÿ����dzȽ���ΪxԪ��ÿ��˯�������Ͻ���ΪyԪ��
�����⣬��![]() ��
��
��ã�![]() ��
��
����ÿ����dzȽ���Ϊ35Ԫ��ÿ��˯�������Ͻ���Ϊ40Ԫ��
��2����������ã�
w����40��35��a+��50��40����200��a������5a+2000��
��3���蹺����dz�a�䣬����˯��������Ϊ��200��a���䣬
��200��a��5a��a��30��
���30��a![]() ��
��
�ɣ�2����w����5a+2000��
�ߩ�5��w��a���������С��
�൱a��30ʱ��y���
����a��30ʱ��w�������5��30+2000��1850��Ԫ����
�𣺵�������dz�30�䣬����˯��������170���ˮ�������̵��ܻ�õ���������������Ϊ1850Ԫ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
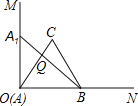
����Ŀ����֪��MON��90�㣬�ȱ�������ABC��һ������B������ON�ϵ�һ���㣬����A�ڵ�O�غϣ�����C�ڡ�MON�ڲ�
(1)����A������OM���ƶ���A1ʱ������A1B�����ڡ�MON�ڲ�������A1BΪһ�ߵĵȱ�������A1BC1(������ͼ�ۼ�����д����)��
(2)��A1B��OC���ڵ�Q��BC���ӳ�����A1C1���ڵ�D����֤����BCQ�ס�BA1D��
(3)����CC1���Բ����BCC1Ϊ���ٶȣ���֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
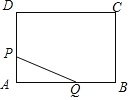
����Ŀ����ͼ������ABCD�У�AB=8cm��BC=6cm����P�ӵ�A��������lcm/s���ٶ���A��D��C���������˶���ͬʱ��Q�ӵ�A��������2cm/s���ٶ���A��B��C���������˶�����һ���㵽���Cʱ����һ����Ҳ��ֹ֮ͣ�����˶�ʱ��Ϊt��s������APQ�����ΪS��cm2���������ܴ��·�ӳS��t֮�亯����ϵ��ͼ���ǣ�������
A. 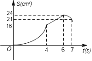 B.
B. 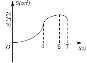 C.
C. 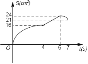 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
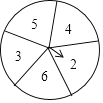
����Ŀ������һ����ͼ��ʾ�ı���2��3��4��5��6��ת�̣��������ŷֱ����1��2��3��4��5���˿ˣ�С����С������������Ϸ������С��ת��ת��һ�Σ�����ָ��ͣ��ʱ��ָ�����֣�����С�������ȡ���泯�ϵ��˿�һ�ţ�������������֣�
��1�����б�������״ͼ�ķ�����������µ���������֮��Ϊ8�ĸ��ʣ�
��2�������µ���������֮��Ϊ��������С����1�֣������µ���������֮��Ϊż������С����1�֣������Ϸ��˫����ƽ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
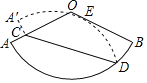
����Ŀ����ͼ����֪����AOB��Բ�Ľ�Ϊ120�㣬��C�ǰ뾶OA��һ�㣬��D��![]() ��һ�㣮������AOB��CD���ۣ�ʹ���۵����ͼ��ǡ����뾶OB�����ڵ�E������OCD��45�㣬OC��
��һ�㣮������AOB��CD���ۣ�ʹ���۵����ͼ��ǡ����뾶OB�����ڵ�E������OCD��45�㣬OC��![]() +1��������AOB�İ뾶���ǣ�������
+1��������AOB�İ뾶���ǣ�������
A. 2+![]() B. 2+
B. 2+![]() C. 2
C. 2![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���д�С���ֻ�����1���������3��С��������������ܺ�Ϊ23�֣�2���������5��С��������������ܺ�Ϊ41��. 1���������1��С�����Ķ�������ֱ�Ϊ���ٶ֣���1��������Ķ������Ϊx�֣�1��С�����Ķ������Ϊy�֣������⣬�����з�����Ϊ__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
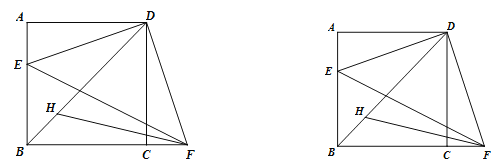
����Ŀ����ͼ����������ABCD�У�E�DZ�AB�ϵ�һ���㣬��F�ڱ�BC���ӳ����ϣ���![]() ������DE��DF��EF. FHƽ��
������DE��DF��EF. FHƽ��![]() ��BD�ڵ�H.
��BD�ڵ�H.
��1����֤��![]() ��
��
��2����֤��![]() ��
��
��3������H��![]() �ڵ�M���õ�ʽ��ʾ�߶�AB��HM��EF֮���������ϵ����֤��.
�ڵ�M���õ�ʽ��ʾ�߶�AB��HM��EF֮���������ϵ����֤��.
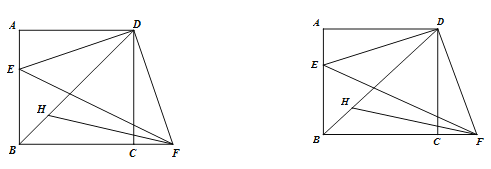
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ1���ڡ�ABC�У���ACB��90�㣬BC��AC����D��AB�ϣ�DE��AB��BC��E����F��AE���е�
��1��д���߶�FD���߶�FC�Ĺ�ϵ��֤����
��2����ͼ2������BDE�Ƶ�B��ʱ����ת����0�㣼����90�㣩�������������䣬�߶�FD���߶�FC�Ĺ�ϵ�Ƿ�仯��д����Ľ��۲�֤����
��3������BDE�Ƶ�B��ʱ����תһ�ܣ����BC��4��BE��2![]() ��ֱ��д���߶�BF�ķ�Χ��
��ֱ��д���߶�BF�ķ�Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������龳�� ��֪���ε����Ϊa��aΪ������a��0�������þ��εij�Ϊ����ʱ�������ܳ���С����Сֵ�Ƕ��٣�
����ѧģ�ͣ�
��þ��εij�Ϊx���ܳ�Ϊy����y��x�ĺ�����ϵʽΪy=2��![]() ����x��0��
����x��0��
��̽���о���
���ǿ��Խ����ǰ�о������ľ��飬��̽������y=![]() ��x��0����ͼ������ʣ�
��x��0����ͼ������ʣ�
��1������д�±�������������ͼ��

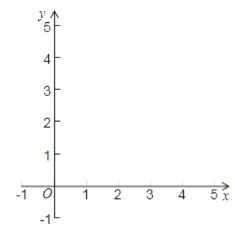
�ڹ۲�ͼ��д���ú���������ͬ���͵����ʣ�
��������κ���y=ax2+bx+c��a��0�������С��ֵʱ������ͨ���۲�ͼ������ͨ���䷽�õ�������ͨ���䷽����y=![]() ��x��0������Сֵ��
��x��0������Сֵ��
������⣺��2����������������������龳���е����⣬ֱ��д���𰸡�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com