
【题目】如图1,点E为矩形ABCD边AD上一点,点P点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为y cm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分).则下列结论:①AD=BE=5cm;②当0<t≤5时,![]() ;③直线NH的解析式为y=
;③直线NH的解析式为y=![]() t+27; ④若△ABE与△QBP相似,则t=
t+27; ④若△ABE与△QBP相似,则t=![]() 秒, 其中正确结论的个数为( )
秒, 其中正确结论的个数为( )


A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
据图(2)可以判断三角形的面积变化分为三段,可以判断出当点P到达点E时点Q到达点C,从而得到BC、BE的长度,再根据M、N是从5秒到7秒,可得ED的长度,然后表示出AE的长度,根据勾股定理求出AB的长度,然后针对各小题分析解答即可.
①根据图(2)可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=5cm,
∴AD=BE=5,故①正确;
②如图1,过点P作PF⊥BC于点F,
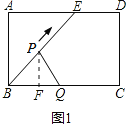
根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB= ![]() ,
,
∴PF=PBsin∠PBF= ![]() t,
t,
∴当0<t≤5时,![]() ,故②正确;
,故②正确;
③根据5-7秒面积不变,可得ED=2,
当点P运动到点C时,面积变为0,此时点P走过的路程为BE+ED+DC=11,
故点H的坐标为(11,0),
设直线NH的解析式为y=kx+b,
将点H(11,0),点N(7,10)代入可得:![]() ,
,
解得: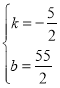 .
.
故直线NH的解析式为:![]() ,故③错误;
,故③错误;
④当△ABE与△QBP相似时,点P在DC上,如图2所示:
∵tan∠PBQ=tan∠ABE= ![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:t= ![]() .故④正确;
.故④正确;
综上可得①②④正确,共3个.
故选:C.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
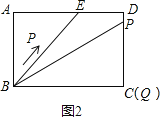
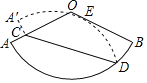
【题目】如图,已知扇形AOB的圆心角为120°,点C是半径OA上一点,点D是![]() 上一点.将扇形AOB沿CD对折,使得折叠后的图形恰好与半径OB相切于点E.若∠OCD=45°,OC=
上一点.将扇形AOB沿CD对折,使得折叠后的图形恰好与半径OB相切于点E.若∠OCD=45°,OC=![]() +1,则扇形AOB的半径长是( )
+1,则扇形AOB的半径长是( )
A. 2+![]() B. 2+
B. 2+![]() C. 2
C. 2![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
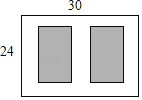
【题目】如图,某小区有一块长为30 m,宽为24 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为________m.
查看答案和解析>>
科目:初中数学 来源: 题型:
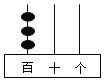
【题目】把3颗算珠放在计数器的3根插棒上构成一个数字,例如,如图摆放的算珠表示数300.现将3颗算珠任意摆放在这3根插棒上.
(1)若构成的数是两位数,则十位数字为1的概率为 ;
(2)求构成的数是三位数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
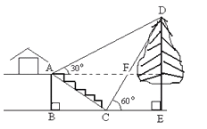
【题目】某校在苏州园林研学时,校综合实践活动小组的同学欲测量公园内一棵树![]() 的高度,他们在这棵树的正前方一座楼亭前的台阶上
的高度,他们在这棵树的正前方一座楼亭前的台阶上![]() 点处测得树顶端
点处测得树顶端![]() 的仰角为
的仰角为![]() ,朝着这棵树的方向走到台阶下的点
,朝着这棵树的方向走到台阶下的点![]() 处,测得树顶端
处,测得树顶端![]() 的仰角为
的仰角为![]() .已知
.已知![]() 点的高度
点的高度![]() 为
为![]() 米,台阶
米,台阶![]() 的坡度为
的坡度为![]() (即
(即![]() ),且
),且![]() 三点在同一条直线上.请根据以上条件求出树
三点在同一条直线上.请根据以上条件求出树![]() 的高度(侧倾器的高度忽略不计).
的高度(侧倾器的高度忽略不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境) 已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
(数学模型)
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(![]() )(x>0)
)(x>0)
(探索研究)
我们可以借鉴以前研究函数的经验,先探索函数y=![]() (x>0)的图象和性质.
(x>0)的图象和性质.
(1)①填写下表,画出函数的图象;

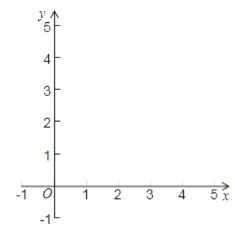
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=![]() (x>0)的最小值.
(x>0)的最小值.
解决问题:(2)用上述方法解决“问题情境”中的问题,直接写出答案。
查看答案和解析>>
科目:初中数学 来源: 题型:
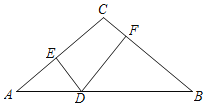
【题目】如图,在等腰三角形ACB中,AC=BC=10,AB=16,D为底边AB上一动点(不与点A,B重合),DE⊥AC,DF⊥BC,垂足分别为点E,F,则DE+DF等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解我市居民的低碳生活状况,适宜采用抽样调查的方法
B. 一组数据2,2,3,6的众数和中位数都是2
C. “掷一枚硬币正面朝上的概率是![]() ”,表示每抛硬币2次就有1次正面朝上
”,表示每抛硬币2次就有1次正面朝上
D. 随机抽取甲乙两名同学的5次数学成绩,平均分都是90分,方差分别是S甲2=5,S乙2=10,说明乙的成绩较为稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂准备生产甲、乙两种商品销往“一带一路”沿线国家和地区.已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.求甲种商品与乙种商品的销售单价各是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com