
ЁОЬтФПЁПЯТУцЪЧаЁЖЋЩшМЦЕФЁАзїЦНааЫФБпаЮвЛБпжаЕуЁБЕФГпЙцзїЭМЙ§ГЬ.
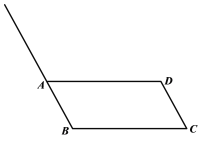
вбжЊЃКЦНааЫФБпаЮABCD.
ЧѓзїЃКЕуMЃЌЪЙЕуMЮЊБпADЕФжаЕу.

зїЗЈЃКШчЭМЃЌ
ЂйзїЩфЯпBAЃЛ
ЂквдЕуAЮЊдВаФЃЌCDГЄЮЊАыОЖЛЛЁЃЌНЛBAЕФбгГЄЯпгкЕуEЃЛ
ЂлСЌНгECНЛADгкЕуMЃЎ
ЫљвдЕуMОЭЪЧЫљЧѓзїЕФЕуЃЎ
ИљОнаЁЖЋЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌ
ЃЈ1ЃЉЪЙгУжБГпКЭдВЙцЃЌВЙШЋЭМаЮЃЈБЃСєзїЭМКлМЃЃЉЃЛ
ЃЈ2ЃЉЭъГЩЯТУцЕФжЄУїЃЎ
жЄУїЃКСЌНгACЃЌEDЃЎ
ЁпЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌ
Ёр![]() ЃЎ
ЃЎ
ЁпAE= ЃЌ
ЁрЫФБпаЮEACDЪЧЦНааЫФБпаЮЃЈ ЃЉЃЈЬюЭЦРэЕФвРОнЃЉЃЎ
Ёр![]() ЃЈ ЃЉЃЈЬюЭЦРэЕФвРОнЃЉЃЎ
ЃЈ ЃЉЃЈЬюЭЦРэЕФвРОнЃЉЃЎ
ЁрЕуMЮЊЫљЧѓзїЕФБпADЕФжаЕуЃЎ
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉЃЉ![]() ЃЛвЛзщЖдБпЦНааЧвЯрЕШЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЛЦНааЫФБпаЮЕФЖдНЧЯпЛЅЯрЦНЗж.
ЃЛвЛзщЖдБпЦНааЧвЯрЕШЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЛЦНааЫФБпаЮЕФЖдНЧЯпЛЅЯрЦНЗж.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтзїЭММДПЩ
ЃЈ2ЃЉИљОнЦНааЫФБпаЮЕФХаЖЈКЭаджЪМДПЩЕУГіД№АИ.
НтЃКЃЈ1ЃЉВЙШЋЕФЭМЯёШчЭМЫљЪОЃК
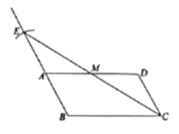
ЃЈ2ЃЉвђЮЊ![]() ЃЌдђвЊЪЙЕУЫФБпаЮEACDЪЧЦНааЫФБпаЮЃЌдђШБЩй
ЃЌдђвЊЪЙЕУЫФБпаЮEACDЪЧЦНааЫФБпаЮЃЌдђШБЩй![]() ЃЌЙЪД№АИЮЊ
ЃЌЙЪД№АИЮЊ![]() ЃЌЭЦРэвРОнЮЊвЛзщЖдБпЦНааЧвЯрЕШЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЛИљОнЦНааЫФБпаЮЕФаджЪПЩжЊЦНааЫФБпаЮЕФЖдНЧЯпЛЅЯрЦНЗж.
ЃЌЭЦРэвРОнЮЊвЛзщЖдБпЦНааЧвЯрЕШЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЛИљОнЦНааЫФБпаЮЕФаджЪПЩжЊЦНааЫФБпаЮЕФЖдНЧЯпЛЅЯрЦНЗж.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћШ§ИіЪ§aЁЂbЁЂcТњзуЦфжавЛИіЪ§ЕФСНБЖЕШгкСэЭтСНИіЪ§ЕФКЭЃЌЮвУЧГЦетШ§ИіЪ§aЁЂbЁЂcЪЧЁАЕШВюЪ§ЁБШєе§БШР§КЏЪ§yЃН2xЕФЭМЯѓЩЯгаШ§ЕуAЃЈ![]() mЉ1ЃЌy1ЃЉЁЂBЃЈmЃЌy2ЃЉЁЂCЃЈ2m+1ЃЌy3ЃЉЃЌЧветШ§ЕуЕФзнзјБъy1ЁЂy2ЁЂy3ЪЧЁАЕШВюЪ§ЁБЃЌдђmЃН_____ЃЎ
mЉ1ЃЌy1ЃЉЁЂBЃЈmЃЌy2ЃЉЁЂCЃЈ2m+1ЃЌy3ЃЉЃЌЧветШ§ЕуЕФзнзјБъy1ЁЂy2ЁЂy3ЪЧЁАЕШВюЪ§ЁБЃЌдђmЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+cЃЈaЃМ0ЃЉгыxжсНЛгкAЃЈЉ2ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌЧвOC=2OAЃЎ
ЃЈ1ЃЉЪдЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉжБЯпy=kx+1ЃЈkЃО0ЃЉгыyжсНЛгкЕуDЃЌгыХзЮяЯпНЛгкЕуPЃЌгыжБЯпBCНЛгкЕуMЃЌМЧm=![]() ЃЌЪдЧѓmЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЛ
ЃЌЪдЧѓmЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕуQЪЧxжсЩЯЕФвЛИіЖЏЕуЃЌЕуNЪЧзјБъЦНУцФкЕФвЛЕуЃЌЪЧЗёДцдкетбљЕФЕуQЁЂNЃЌЪЙЕУвдPЁЂDЁЂQЁЂNЫФЕузщГЩЕФЫФБпаЮЪЧОиаЮЃПШчЙћДцдкЃЌЧыЧѓГіЕуNЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
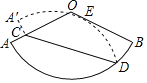
ЁОЬтФПЁПШчЭМЃЌвбжЊЩШаЮAOBЕФдВаФНЧЮЊ120ЁуЃЌЕуCЪЧАыОЖOAЩЯвЛЕуЃЌЕуDЪЧ![]() ЩЯвЛЕуЃЎНЋЩШаЮAOBбиCDЖделЃЌЪЙЕУелЕўКѓЕФЭМаЮЧЁКУгыАыОЖOBЯрЧагкЕуEЃЎШєЁЯOCDЃН45ЁуЃЌOCЃН
ЩЯвЛЕуЃЎНЋЩШаЮAOBбиCDЖделЃЌЪЙЕУелЕўКѓЕФЭМаЮЧЁКУгыАыОЖOBЯрЧагкЕуEЃЎШєЁЯOCDЃН45ЁуЃЌOCЃН![]() +1ЃЌдђЩШаЮAOBЕФАыОЖГЄЪЧЃЈЁЁЁЁЃЉ
+1ЃЌдђЩШаЮAOBЕФАыОЖГЄЪЧЃЈЁЁЁЁЃЉ
A. 2+![]() B. 2+
B. 2+![]() C. 2
C. 2![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊПЊПкЯђЯТЕФХзЮяЯпyЃНax2Љ2ax+3гыxжсЕФНЛЕуЮЊAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓБпЃЉЃЌгыyжсЕФНЛЕуЮЊCЃЌOCЃН3OA
ЃЈ1ЃЉЧыжБНгаДГіИУХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЃЌDЮЊХзЮяЯпЕФЖЅЕуЃЌСЌНгBDЁЂBCЃЌPЮЊЖдГЦжсгвВрХзЮяЯпЩЯвЛЕуЃЎШєЁЯABDЃНЁЯBCPЃЌЧѓЕуPЕФзјБъ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌMЁЂNЪЧХзЮяЯпЩЯЕФЖЏЕуЃЎШєЁЯMPNЃН90ЁуЃЌжБЯпMNБиЙ§вЛЖЈЕуЃЌЧыЧѓГіИУЖЈЕуЕФзјБъЃЎ
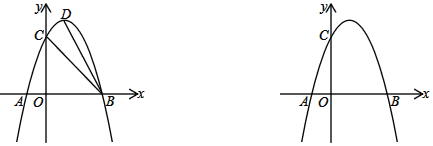
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
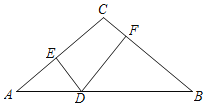
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌEЪЧБпABЩЯЕФвЛЖЏЕуЃЌЕуFдкБпBCЕФбгГЄЯпЩЯЃЌЧв![]() ЃЌСЌНгDEЃЌDFЃЌEF. FHЦНЗж
ЃЌСЌНгDEЃЌDFЃЌEF. FHЦНЗж![]() НЛBDгкЕуH.
НЛBDгкЕуH.
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃК
ЃК
ЃЈ3ЃЉЙ§ЕуHзї![]() гкЕуMЃЌгУЕШЪНБэЪОЯпЖЮABЃЌHMгыEFжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУї.
гкЕуMЃЌгУЕШЪНБэЪОЯпЖЮABЃЌHMгыEFжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУї.
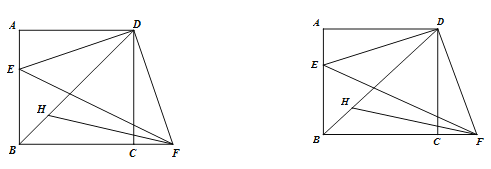
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOAЁЭOBЃЌABЁЭxжсгкЕуCЃЌЕуAЃЈ![]() ЃЌ1ЃЉдкЗДБШР§КЏЪ§y=
ЃЌ1ЃЉдкЗДБШР§КЏЪ§y=![]() ЕФЭМЯёЩЯЃЎ
ЕФЭМЯёЩЯЃЎ
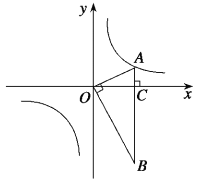
ЃЈ1ЃЉk= ЃЛ
ЃЈ2ЃЉдкxжсЕФИКАыжсЩЯДцдквЛЕу P ЃЌЪЙЕУSЁїAOP=![]() SЁїAOBЃЌЧѓЕуPЕФзјБъЃЛ
SЁїAOBЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШєНЋЁїBOAШЦЕуBАДФцЪБеыЗНЯђа§зЊ60ЁуЕУЕНЁїBDEЃЌжБНгаДГіЕуEЕФзјБъЃЌВЂХаЖЯЕуEЪЧЗёдкИУЗДБШР§КЏЪ§ЕФЭМЯёЩЯЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
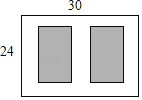
ЁОЬтФПЁПШчЭМЃЌФГаЁЧјгавЛПщГЄЮЊ30 mЃЌПэЮЊ24 mЕФОиаЮПеЕиЃЌМЦЛЎдкЦфжааоНЈСНПщЯрЭЌЕФОиаЮТЬЕиЃЌЫќУЧЕФУцЛ§жЎКЭЮЊ480 m2ЃЌСНПщТЬЕижЎМфМАжмБпгаПэЖШЯрЕШЕФШЫааЭЈЕРЃЌдђШЫааЭЈЕРЕФПэЖШЮЊ________mЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќШ§НЧаЮACBжаЃЌACЃНBCЃН10ЃЌABЃН16ЃЌDЮЊЕзБпABЩЯвЛЖЏЕу(ВЛгыЕуAЃЌBжиКЯ)ЃЌDEЁЭACЃЌDFЁЭBCЃЌДЙзуЗжБ№ЮЊЕуEЃЌFЃЌдђDE+DFЕШгк_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com