
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c��a��0����x�ύ��A����2��0����B��4��0�����㣬��y�ύ�ڵ�C����OC=2OA��
��1�����������ߵĽ���ʽ��
��2��ֱ��y=kx+1��k��0����y�ύ�ڵ�D���������߽��ڵ�P����ֱ��BC���ڵ�M����m=![]() ������m�����ֵ����ʱ��P�����ꣻ
������m�����ֵ����ʱ��P�����ꣻ
��3���ڣ�2���������£���Q��x���ϵ�һ�����㣬��N������ƽ���ڵ�һ�㣬�Ƿ���������ĵ�Q��N��ʹ����P��D��Q��N�ĵ���ɵ��ı����Ǿ��Σ�������ڣ��������N�����ꣻ��������ڣ���˵�����ɣ�

���𰸡���1��y=��![]() ��x+2����x��4����y=��
��x+2����x��4����y=��![]() x2+x+4��y=��
x2+x+4��y=��![]() ��x��1��2+
��x��1��2+![]() ����2�����ֵΪ
����2�����ֵΪ![]() ����ʱP��2��4������3����
����ʱP��2��4������3����![]() ��3����6����3����
��3����6����3����
�������������������1���������ߵĽ���ʽΪy=a��x+2����x��4����������֪������õ�C������������ʽ���aֵ�����ɵ������ߵĽ���ʽ����2����PE��x����E����BC��F����֤��CMD�ס�FMP���������������ε����ʿɵ�m=![]() ����P��n����
����P��n����![]() n2+n+4������F��n����n+4������n��ʾ��PF�ij����Ӷ��õ�m��n�Ķ��κ�����ϵʽ�����ö��κ��������ʽ�����⼴�ɣ���3�����������ĵ�Q��N��ʹ����P��D��Q��N�ĵ���ɵ��ı����Ǿ��Σ���DP�Ǿ��εıߺ�DP�Ǿ��εĶԽ�������������N������.
n2+n+4������F��n����n+4������n��ʾ��PF�ij����Ӷ��õ�m��n�Ķ��κ�����ϵʽ�����ö��κ��������ʽ�����⼴�ɣ���3�����������ĵ�Q��N��ʹ����P��D��Q��N�ĵ���ɵ��ı����Ǿ��Σ���DP�Ǿ��εıߺ�DP�Ǿ��εĶԽ�������������N������.
���������
��1����Ϊ������y=ax2+bx+c����A����2��0����B��4��0�����㣬��y=a��x+2����x��4����
��OC=2OA��OA=2��
��C��0��4�������������ߵĽ���ʽ�õ�a=��![]() ��
��
��y=��![]() ��x+2����x��4����y=��
��x+2����x��4����y=��![]() x2+x+4��y=��
x2+x+4��y=��![]() ��x��1��2+
��x��1��2+![]() ��
��
��2����ͼ1�У���PE��x����E����BC��F��
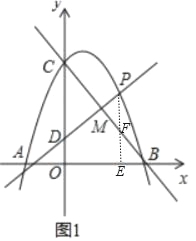
��CD��PE��
���CMD�ס�FMP��
��m=![]() =
=![]() ��
��
��ֱ��y=kx+1��k��0����y�ύ�ڵ�D����D��0��1����
��BC�Ľ���ʽΪy=��x+4��
��P��n����![]() n2+n+4������F��n����n+4����
n2+n+4������F��n����n+4����
��PF=��![]() n2+n+4������n+4��=��
n2+n+4������n+4��=��![]() ��n��2��2+2��
��n��2��2+2��
��m=![]() =��
=��![]() ��n��2��2+
��n��2��2+![]() ��
��
�ߩ�![]() ��0��
��0��
����n=2ʱ��m�����ֵ�����ֵΪ![]() ����ʱP��2��4����
����ʱP��2��4����
��3�����������ĵ�Q��N��ʹ����P��D��Q��N�ĵ���ɵ��ı����Ǿ��Σ�
����DP�Ǿ��εı�ʱ�����������Σ�
a����ͼ2��1�У��ı���DQNP�Ǿ���ʱ��

�У�2����֪P��2��4��������y=kx+1�У��õ�k=![]() ��
��
��ֱ��DP�Ľ���ʽΪy=![]() x+1���ɵ�D��0��1����E����
x+1���ɵ�D��0��1����E����![]() ��0����
��0����
����DOE�ס�QOD�ɵ�![]() =
=![]() ��
��
��OD2=OEOQ��
��1=![]() OQ��
OQ��
��OQ=![]() ��
��
��Q��![]() ��0����
��0����
���ݾ��ε����ʣ�����P����ƽ��![]() ����λ������ƽ��1����λ�õ���N��
����λ������ƽ��1����λ�õ���N��
��N��2+![]() ��4��1������N��
��4��1������N��![]() ��3��
��3��
b����ͼ2��2�У��ı���PDNQ�Ǿ���ʱ��
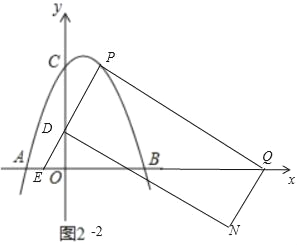
��ֱ��PD�Ľ���ʽΪy=![]() x+1��PQ��PD��
x+1��PQ��PD��
��ֱ��PQ�Ľ���ʽΪy=��![]() x+
x+![]() ��
��
��Q��8��0����
���ݾ��ε����ʿ�֪������D����ƽ��6����λ������ƽ��4����λ�õ���N��
��N��0+6��1��4������N��6����3����
����DP�ǶԽ���ʱ����Q��x��0������QD2=x2+1��QP2=��x��2��2+42��PD2=13��
��Q��ֱ�Ƕ��㣬
��QD2+QP2=PD2��
��x2+1+��x��2��2+16=13��
������x2��2x+4=0�������⣬�������β����ڣ�
�������������������ĵ�N����Ϊ��![]() ��3����6����3����
��3����6����3����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ������һ�����ܵƣ���֪1ֻA�ͽ��ܵƺ�3ֻB�ͽ��ܵƹ���26Ԫ��3ֻA�ͽ��ܵƺ�2ֻB�ͽ��ܵƹ���29Ԫ��
��1����һֻA�ͽ��ܵƺ�һֻB�ͽ��ܵƵ��ۼ۸��Ƕ���Ԫ��
��2��ѧУ�������������ͺŵĽ��ܵƹ�50ֻ������A�ͽ��ܵƵ�����������B�ͽ��ܵ�������3��������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˽���������Դ�Χ���������ij���Ӱ���Լ�Ӧ�Դ�ʩ�Ŀ���������һ�γ������飬����������Ϊ�ĸ��ȼ���A���dz��˽⣺B���Ƚ��˽⣺C�������˽⣻D�����˽⣮���ݵ���ͳ�ƽ���������˲�����������ͳ��ͼ��������ͳ��ͼ�����ش��������⣺
���������˽�̶� | �ٷֱ� | |
A | �dz��˽� | 5% |
B | �Ƚ��˽� | m% |
C | �����˽� | 45% |
D | ���˽� | n% |
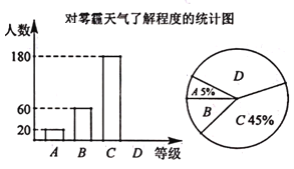
��1�����β�������������________�ˣ�m=________��n=________��
��2��ͳ��ͼ������D��Բ�Ľ���________��.
��3��ijУ����չ����������֪ʶ�������ţ�3����֣��ʦ����2��������1��Ů������ѡ2�˲μӱ�������ǡ��ѡ����1��1Ů���ĸ��ʣ�Ҫ���б�����״ͼ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦΪ�˽�ijУѧ�������ѧ��ǰԤϰ�ľ���������Բ���ѧ�������˸��ٵ��飬������������Ϊ���࣬A���ܺã�B���Ϻã�C��һ�㣻D���ϲ���Ƴ�����ͳ��ͼ��
��1������ʦһ�������˶�����ͬѧ��������������ͳ��ͼ����������
��2������У��1000��ѧ��������ѧ��ǰԤϰ���ܺá��͡��Ϻá��ܹ�Լ�����ˣ�
��3��Ϊ�˹�ͬ����������ʦ��ӱ������A���D��ѧ���и����ѡȡһλͬѧ���С�һ��һ������ѧϰ�������ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�ĸ��ʣ���Ҫ���б�����״ͼ��
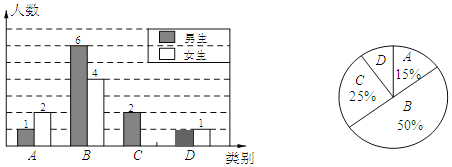
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��֯���꼶ѧ���μӺ�����д�������������ȡ����ѧ���ɼ���Ϊ�������з��������Ƴ����µ�ͳ�Ʊ���
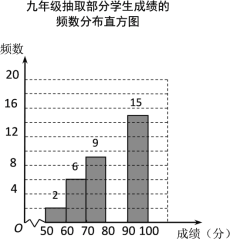
![]()
�ɼ�x/�� | Ƶ�� | Ƶ�� | |
��1�� | x��60 | 2 | 0.04 |
��2�� | 60��x��70 | 6 | 0.12 |
��3�� | 70��x��80 | 9 | b |
��4�� | 80��x��90 | a | 0.36 |
��5�� | 90��x��100 | 15 | 0.30 |
�����������Ϣ������������⣺
��1��a��______��b��______��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�������У�����ѧ���ɼ�����λ�����ڵ�_______����
��4����֪���꼶��400��ѧ���μ���α��������ɼ���90�����ϣ���90�֣���Ϊ�������Ƹ��꼶�ɼ�Ϊ�ŵ��ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Rt��ABC�ı�ABΪֱ������ABC�����Բ��O����B��ƽ����BE��AC��D������O��E����E��EF��AC��BA���ӳ�����F��
��1����֤��EF�ǡ�O���ߣ�
��2����AB=15��EF=10����AE�ij���
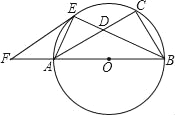
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ũ����ֲר��ָ��ƶ������ֲ��������棬�ջ�ĺ�����������Ƚ������ˮ���г�����֪ijˮ�������̹����˺������������ˮ����10�䣬����������ļס����������۵꣨�ֱ��Ƽꡢ�ҵ꣩���ۣ�Ԥ��ÿ��ˮ����ӯ��������
����/�� | ����/�� | |
�� | 22Ԫ | 34Ԫ |
�ҵ� | 18Ԫ | 26Ԫ |
��1�����ס�����������10�䣬���м������2�䣬����8�䣻�ҵ������8�䣬����2�䣬����������������ӯ������Ԫ��
��2�����ס�����������10�䣬���ڱ�֤�ҵ�ӯ����С��200Ԫ�������£�������Ƴ�ʹˮ��������ӯ���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С����Ƶġ���ƽ���ı���һ���е㡱�ij߹���ͼ����.
��֪��ƽ���ı���ABCD.
��������M��ʹ��MΪ��AD���е�.

��������ͼ��
��������BA��
���Ե�AΪԲ�ģ�CD��Ϊ�뾶��������BA���ӳ����ڵ�E��
������EC��AD�ڵ�M��
���Ե�M�����������ĵ㣮
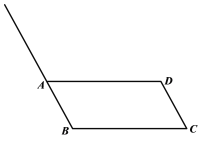
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ�������ͼ�ۼ�����
��2����������֤����
֤��������AC��ED��
���ı���ABCD��ƽ���ı��Σ�
��![]() ��
��
��AE= ��
���ı���EACD��ƽ���ı��Σ� ���������������ݣ���
��![]() �� ���������������ݣ���
�� ���������������ݣ���
����MΪ�������ı�AD���е㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���A��C��F���������ϣ�E��OA���е㣬�ı���AOCB�Ǿ��Σ��ı���BDEF�������Σ�����C������Ϊ��3��0�������D������Ϊ��������
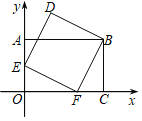
A. ��1��2.5��B. ��1��1+ ![]() ��C. ��1��3��D. ��
��C. ��1��3��D. ��![]() ��1��1+
��1��1+ ![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com