
【题目】某报社为了解温州市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解:B.比较了解:C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题:
对雾霾的了解程度 | 百分比 | |
A | 非常了解 | 5% |
B | 比较了解 | m% |
C | 基本了解 | 45% |
D | 不了解 | n% |
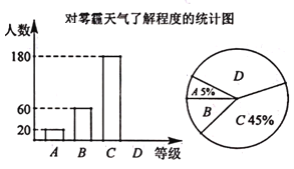
(1)本次参与调查的市民共有________人,m=________,n=________.
(2)统计图中扇形D的圆心角是________度.
(3)某校准备开展关于雾霾的知识竞赛,九(3)班郑老师欲从2名男生和1名女生中任选2人参加比赛,求恰好选中“1男1女”的概率(要求列表或画树状图).
【答案】(1)400;15;35;(2)126;(3)![]()
【解析】
(1)利用本次参与调查的市民人数=A等级的人数÷对应的百分比;用比较了解的人数除以总人数,求出m的值,再用整体1减去其它对雾霾的了解程度的百分比,从而求出n的值.
(2)利用扇形统计图中D部分扇形所对应的圆心角=360°×D类的百分比.
(3)画树状图展示所有6种等可能的结果数,再找出恰好选中1男1女的结果数,然后根据概率公式求解.
(1)本次参与调查的市民共有:20÷5%=400(人),
m%=![]() ×100%=15%,则m=15,
×100%=15%,则m=15,
n%=1-5%-45%-15%=35%,则n=35;
故答案为400,15,35;
(2)扇形统计图中D部分扇形所对应的圆心角是360°×35%=126°.
故答案为126;
(3)根据题意画图如下:
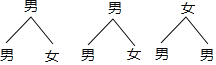
共有6种等可能的结果数,其中恰好选中1男1女的结果数为4种,
所以恰好选中1男1女的概率是![]() .
.


科目:初中数学 来源: 题型:
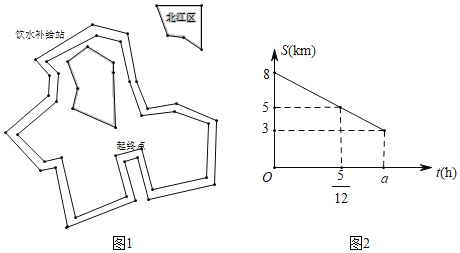
【题目】“2019宁波国际山地马拉松赛”于2019年3月31日在江北区举行,小林参加了环绕湖8km的迷你马拉松项目(如图1),上午8:00起跑,赛道上距离起点5km处会设置饮水补给站,在比赛中,小林匀速前行,他距离终点的路程s(km)与跑步的时间t(h)的函数图象的一部分如图2所示
(1)求小林从起点跑向饮水补给站的过程中与t的函数表达式
(2)求小林跑步的速度,以及图2中a的值
(3)当跑到饮水补给站时,小林觉得自己跑得太悠闲了,他想挑战自己在上午8:55之前跑到终点,那么接下来一段路程他的速度至少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:

请你根据统计图回答下列问题:
(1)喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;
(2)请你估计全校500名学生中最喜欢“排球”项目的有多少名?
(3)在扇形统计图中,“篮球”部分所对应的圆心角是多少度?
(4)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三个数a、b、c满足其中一个数的两倍等于另外两个数的和,我们称这三个数a、b、c是“等差数”若正比例函数y=2x的图象上有三点A(![]() m﹣1,y1)、B(m,y2)、C(2m+1,y3),且这三点的纵坐标y1、y2、y3是“等差数”,则m=_____.
m﹣1,y1)、B(m,y2)、C(2m+1,y3),且这三点的纵坐标y1、y2、y3是“等差数”,则m=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-x+2分别交x轴、y轴于点A,B,点D在BA的延长线上,OD的垂直平分线交线段AB于点C.若△OBC和△OAD的周长相等,则OD的长是( )
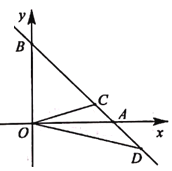
A. 2B. 2![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小芳在本学期的体育测试中,1分钟跳绳获得了满分,她的“满分秘籍”如下:前20秒由于体力好,小芳速度均匀增加,20秒至50秒保持跳绳速度不变,后10秒进行冲刺,速度再次均匀增加,最终获得满分,反映小芳1分钟内跳绳速度y(个/秒)与时间t(秒)关系的函数图象大致为( )

A. A B. B C. C D. D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y=![]() 在第一象限图象上一点,连接OA,过点A作AB∥x轴(点B在点A右侧),连接OB,若OB平分∠AOX,且点B的坐标是(8,4),则k的值是( )
在第一象限图象上一点,连接OA,过点A作AB∥x轴(点B在点A右侧),连接OB,若OB平分∠AOX,且点B的坐标是(8,4),则k的值是( )

A.6B.8C.12D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)试求抛物线的解析式;
(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=![]() ,试求m的最大值及此时点P的坐标;
,试求m的最大值及此时点P的坐标;
(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图像上.
的图像上.
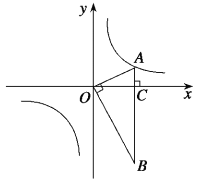
(1)k= ;
(2)在x轴的负半轴上存在一点 P ,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE,直接写出点E的坐标,并判断点E是否在该反比例函数的图像上,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com