
分析 求$\sqrt{(x-3)^{2}+4}$+$\sqrt{{x}^{2}+1}$的最小值,也就是求$\sqrt{(x-3)^{2}+(0-2)^{2}}$+$\sqrt{(x-0)^{2}+(0-1)^{2}}$的最小值,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则$\sqrt{(x-0)^{2}+(0-1)^{2}}$可以看成点P与点A(0,1)的距离,$\sqrt{(x-3)^{2}+(0-2)^{2}}$可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,所以PA′+PB的最小值为线段A′B的长度.
解答 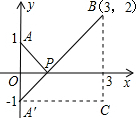 解:∵求$\sqrt{(x-3)^{2}+4}$+$\sqrt{{x}^{2}+1}$的最小值,
解:∵求$\sqrt{(x-3)^{2}+4}$+$\sqrt{{x}^{2}+1}$的最小值,
也就是求$\sqrt{(x-3)^{2}+(0-2)^{2}}$+$\sqrt{(x-0)^{2}+(0-1)^{2}}$的最小值,
如图,建立平面直角坐标系,点P(x,0)是x轴上一点,
∴$\sqrt{(x-0)^{2}+(0-1)^{2}}$可以看成点P与点A(0,1)的距离,$\sqrt{(x-3)^{2}+(0-2)^{2}}$可以看成点P与点B(3,2)的距离,
∴原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,
∵求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,
∴PA′+PB的最小值为线段A′B的长度,
为此,构造直角三角形A′CB,
∵A′C=3,CB=3,
∴A′B=3$\sqrt{2}$,
即原式的最小值为3$\sqrt{2}$.
点评 本题考查了轴对称-最短距离问题,勾股定理,正确的画出图形是解题的关键.


科目:初中数学 来源: 题型:选择题
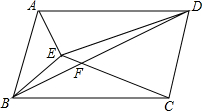 如图,点E在平行四边形ABCD内,连结EA、EB、EC、ED,其中EC与对角线BD交于点F,则S△ABE+S△DEF=( )
如图,点E在平行四边形ABCD内,连结EA、EB、EC、ED,其中EC与对角线BD交于点F,则S△ABE+S△DEF=( )| A. | S△AED | B. | S△ECD | C. | $\frac{1}{4}$S?ABCD | D. | S△BCF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
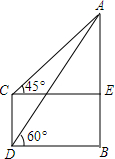 如图,某电视塔AB和楼CD的水平距离为100m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高为73.2m和楼高173.2m.(精确到0.1m)
如图,某电视塔AB和楼CD的水平距离为100m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高为73.2m和楼高173.2m.(精确到0.1m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com