
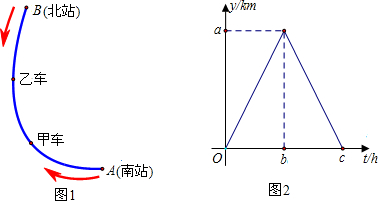
分析 (1)根据题意和函数图象可以得到a、b、c的值;
(2)根据题意和(1)中的答案可以分别求得当0≤t≤3及3<t≤6时,y乙与时间t之间的函数关系式;
(3)根据题意可以画出相应的函数图象,根据函数图象可以得到在整个行驶过程中两车相遇的次数.
解答 解:(1)由题意可和函数图象可得,
a=120,b=120÷40=3,c=2×3=6,
故答案为:120,3,6;
(2)当0≤t≤3时,设y乙与时间t之间的函数关系式为:y乙=kt+b,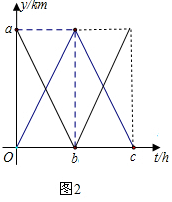
$\left\{\begin{array}{l}{b=120}\\{3k+b=0}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-40}\\{b=120}\end{array}\right.$,
即当0≤t≤3时,y乙与时间t之间的函数关系式为:y乙=-40t+120;
当3<t≤6时,设y乙与时间t之间的函数关系式为:y乙=mt+n,
$\left\{\begin{array}{l}{3m+n=0}\\{6m+n=120}\end{array}\right.$,得$\left\{\begin{array}{l}{m=40}\\{n=-120}\end{array}\right.$,
即当3<t≤6时,y乙与时间t之间的函数关系式为:y乙=40t-120;
(3)y乙与t之间的函数图象如右图2所示,
由图象可知,整个行驶过程中两车相遇次数为2.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
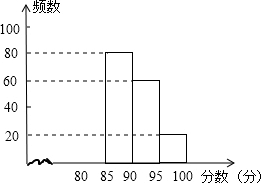 某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | b |
| 90≤x<95 | 60 | c |
| 95≤x<100 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com