
 在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.分析 (1)利用抛物线的顶点F的坐标为(6,2.8),将点(0,2)代入解析式求出即可;
(2)利用当x=9时,y=-$\frac{1}{45}$(x-6)2+2.8=2.6,当y=0时,-$\frac{1}{45}$(x-6)2+2.8=-0.4,分别得出即可;
(3)设抛物线解析式为y=a(x-6)2+h,由点C(0,2)得解析式为y=$\frac{2-h}{36}$(x-6)2+h,再依据x=18时y≤0即可得h的范围.
解答 解:(1)由题意可得抛物线的顶点F的坐标为(6,2.8),
设抛物线的解析式为y=a(x-6)2+2.8,
将点C(0,2)代入,得:36a+2.8=2,
解得:a=-$\frac{1}{45}$,
∴y=-$\frac{1}{45}$(x-6)2+2.8;
(2)当x=9时,y=-$\frac{1}{45}$(9-6)2+2.8=2.6>2.24,
当x=18时,y=-$\frac{1}{45}$(18-6)2+2.8=-0.4<0,
∴这次发球可以过网且不出边界;
(3)设抛物线解析式为y=a(x-6)2+h,
将点C(0,2)代入,得:36a+h=2,即a=$\frac{2-h}{36}$,
∴此时抛物线解析式为y=$\frac{2-h}{36}$(x-6)2+h,
根据题意,得:$\frac{144(2-h)}{36}$+h≤0,
解得:h≥$\frac{8}{3}$,
又∵h>2.32,
∴h≥$\frac{8}{3}$
答:球既能过网又不会出界的h的取值范围是h≥$\frac{8}{3}$.
点评 此题主要考查了二次函数的应用题,求范围的问题,可以利用临界点法求出自变量的值,再根据题意确定范围.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
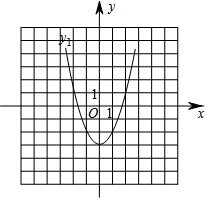 如图为抛物线y1=x2-3,且抛物线y2是由抛物线y1向右平移2个单位得到的.
如图为抛物线y1=x2-3,且抛物线y2是由抛物线y1向右平移2个单位得到的.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
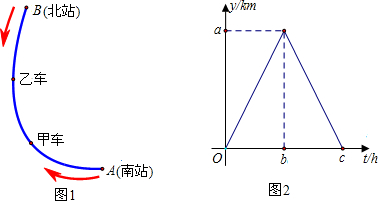
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
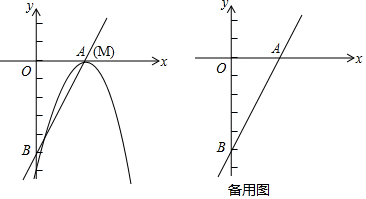
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com