
分析 (1)根据销售量由原销量-因价格上涨而减少的销量可得;
(2)根据利润=销售量×每件的利润,即可解决问题,根据题意确定自变的取值范围,再根据二次函数的性质,即可解决问题;
(3)设取用资金为a元,先表示出两种方案的获取利润表达式,再分类讨论可得.
解答 解:(1)根据题意,得:销售单价为x元时,销售量为600-10(x-40)=1000-10x;
(2)由题意可得,
w=(x-30)[600-(x-40)×10]
化简,得w=-10x2+1300x-30000
即w与x的函数关系式是:w=-10x2+1300x-30000=-10(x-65)2+12250,
∵$\left\{\begin{array}{l}{x≥44}\\{1000-10x≥450}\end{array}\right.$,
∴44≤x≤55,
∴当x=55时,Wmax=11250;
(3)设取用资金为a元,则:
y1=a(1+15%)(1+10%)-a=0.265a;
y2=a(1+30%)-350-a=0.3a-350;
当y1=y2时,即0.265a=0.3a-350,解得a=10000,此时获利相同;
当y1>y2时,即0.265a>0.3a-350,解得a<10000,此时①获利多;
当y1<y2时,即0.265a<0.3a-350,解得10000<a<11250,此时②获利多.
点评 本题考查二次函数的应用,解题的关键是理解题意,搞清楚销售量与售价之间的关系,学会构建二次函数解决最值问题,注意自变量的取值范围.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
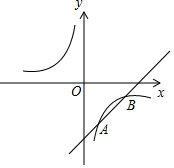 如图,已知一次函数y=kx+b与反比例函数y=$\frac{m}{x}$交于A(1,-3),B(a,-1)两点.
如图,已知一次函数y=kx+b与反比例函数y=$\frac{m}{x}$交于A(1,-3),B(a,-1)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
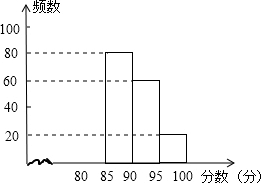 某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | b |
| 90≤x<95 | 60 | c |
| 95≤x<100 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
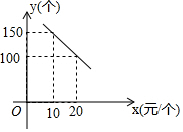 某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示.
某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.
在2016年巴西里约奥运会上,中国女排克服重重困难,凭借顽强的毅力和超强的实力先后战胜了实力同样超强的巴西队,荷兰队和塞尔维亚队,获得了奥运冠军,为祖国和人民争了光.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com