
【题目】如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C的点,且DE2=DBDA,延长AE至F,使得AE=EF,设BF=5,cos∠BED=![]() .
.
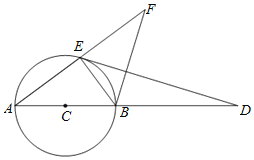
(1)求证:△DEB∽△DAE;
(2)求DA、DE的长;
(3)若点F在B、E、M三点确定的圆上,求MD的长.
【答案】(1)见解析;(2)AD=![]() ,ED=
,ED=![]() ;(3)
;(3)![]()
【解析】
(1)利用两边成比例夹角相等两三角形相似证明即可.
(2)由![]() ,即:
,即: ![]() ,即可求解.
,即可求解.
(3)在△BED中,过点B作HB⊥ED于点H,设HD=x,利用勾股定理构建方程解决问题即可.
解:(1)∵DE2=DBDA,
∴![]() ,
,
又∵∠D=∠D,
∴△DEB∽△DAE.
(2)∵△DEB∽△DAE,
∴∠DEB=∠DAE=α,
∵AB是直径,
∴∠AEB=90°,又AE=EF,
∴AB=BF=5,
∴∠BFE=∠BAE=α,则BF⊥ED交于点H,
∵![]() ,则BE=3,AE=4
,则BE=3,AE=4
∴![]() ,即:
,即:![]()
解得: ![]()
则AD=AB+BD=![]() ,
,
ED=![]() .
.
(3)由点F在B、E、M三点确定的圆上,则BF是该圆的直径,连接MF,
∵BF⊥ED,∠BMF=90°,∴∠MFB=∠D=β,
在△BED中,过点B作HB⊥ED于点H,
设HD=x,则![]()
则![]()
解得: ![]()
则![]() ,则
,则![]()
![]()
DM=BD﹣MB=![]() .
.



 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】关于反比例函数y=﹣![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.图象在第一、三象限B.图象经过点(2,﹣8)
C.当x>0时,y随x的增大而减小D.当x<0时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究问题:
⑴方法感悟:
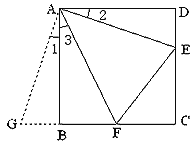
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45°
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,
∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
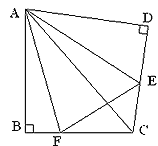
⑵方法迁移:
如图②,将![]() 沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=
沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=![]() ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
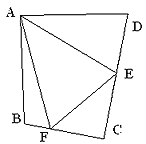
⑶问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足![]() ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由)
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由)
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=10,P为射线AB上一点,连接PD、AC,且PD、AC交于点E,过点A作AF⊥PD,垂足为点F.
(1)当点F落在BC边上时,求AP的值
(2)当△PAE为等腰三角形时,求AP的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近端午,某超市准备购进某品牌的白粽、豆沙粽、蛋黄粽,三种品种的粽子共1000袋(每袋均为同一品种的粽子),其中白粽每袋12个,豆沙粽每袋8个,蛋黄粽每袋6个.为了推广,超市还计划将三个品种的粽子各取![]() 出来,拆开后重新组合包装,制成A、B两种套装进行特价销售:A套装为每袋白粽4个,豆沙粽4个;B套装为每袋白粽4个,蛋黄粽2个,取出的袋数和套装的袋数均为正整数.若蛋黄粽的进货量不低于总进货量的
出来,拆开后重新组合包装,制成A、B两种套装进行特价销售:A套装为每袋白粽4个,豆沙粽4个;B套装为每袋白粽4个,蛋黄粽2个,取出的袋数和套装的袋数均为正整数.若蛋黄粽的进货量不低于总进货量的![]() ,则豆沙粽最多购进__袋.
,则豆沙粽最多购进__袋.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到________元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com