
【题目】探究问题:
⑴方法感悟:
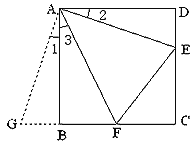
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45°
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,
∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
⑵方法迁移:
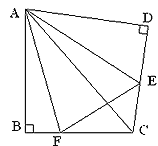
如图②,将![]() 沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=
沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=![]() ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
⑶问题拓展:
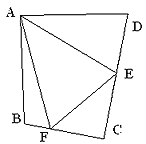
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足![]() ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由)
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由)
.
【答案】⑴EAF、△EAF、GF;⑵DE+BF=EF;⑶当∠B与∠D互补时,可使得DE+BF=EF.
【解析】
(1)根据正方形性质填空;(2)假设∠BAD的度数为![]() ,将△ADE绕点A顺时针旋转
,将△ADE绕点A顺时针旋转![]() 得到△ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,结合正方形性质可得DE+BF=EF. ⑶根据题意可得,当∠B与∠D互补时,可使得DE+BF=EF.
得到△ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,结合正方形性质可得DE+BF=EF. ⑶根据题意可得,当∠B与∠D互补时,可使得DE+BF=EF.
⑴EAF、△EAF、GF.
⑵DE+BF=EF,理由如下:
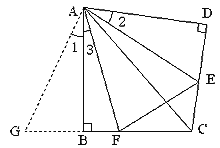
假设∠BAD的度数为![]() ,将△ADE绕点A顺时针旋转
,将△ADE绕点A顺时针旋转![]() 得到△ABG,此时AB与AD重合,由旋转可得:
得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=![]()
∴∠2+∠3=∠BAD-∠EAF=![]()
∵∠1=∠2,
∴∠1+∠3=![]() .
.
即∠GAF=∠EAF
又AG=AE,AF=AF
∴△GAF≌△EAF.
∴GF=EF,
又∵GF=BG+BF=DE+BF
∴DE+BF=EF.
⑶当∠B与∠D互补时,可使得DE+BF=EF.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() .
.
(1)当![]() 时,
时,
①抛物线![]() 的对称轴为
的对称轴为![]() ________;
________;
②若在抛物线![]() 上有两点
上有两点![]() ,且
,且![]() ,则
,则![]() 的取值范围是________;
的取值范围是________;
(2)抛物线![]() 的对称轴与
的对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,将点
轴对称,将点![]() 向右平移3个单位得到点
向右平移3个单位得到点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 恰有一个公共点,结合图象,求
恰有一个公共点,结合图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
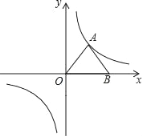
【题目】如图,在反比例函数图象中,△AOB是等边三角形,点A在双曲线的一支上,将△AOB绕点O顺时针旋转α (0°<α<360° ),使点A仍在双曲线上,则α=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点![]() 和点
和点![]() 分别在
分别在![]() 轴和
轴和![]() 轴的正半轴上,
轴的正半轴上,![]() 的平分线与正比例函数
的平分线与正比例函数![]() 交于点
交于点![]() ,且与
,且与![]() 相交于点
相交于点![]() ,在
,在![]() 轴负半轴上有一点
轴负半轴上有一点![]() .
.
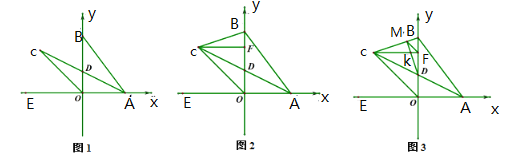
(1)如图1,求证:![]() ;
;
(2)如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
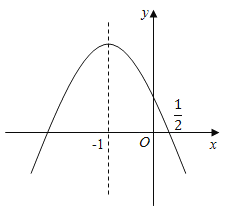
【题目】如图,抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点(![]() ,0),有下列结论:①abc>0; ②a﹣2b+4c>0;③25a﹣10b+4c=0;④3b+2c>0;其中所有正确的结论是( )
,0),有下列结论:①abc>0; ②a﹣2b+4c>0;③25a﹣10b+4c=0;④3b+2c>0;其中所有正确的结论是( )
A.①③B.①③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民上班时常用交通工具的状况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如图所示的尚不完整的统计图:

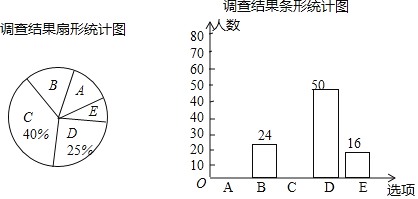
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形B的圆心角度数是 ;
(3)请补全条形统计图;
(4)若该市“上班族”约有15万人,请估计乘公交车上班的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C的点,且DE2=DBDA,延长AE至F,使得AE=EF,设BF=5,cos∠BED=![]() .
.
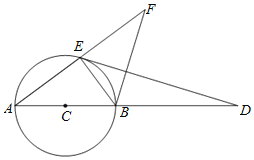
(1)求证:△DEB∽△DAE;
(2)求DA、DE的长;
(3)若点F在B、E、M三点确定的圆上,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线![]() 向左平移2个单位,再向上平移4个单位得到一个新的抛物线.
向左平移2个单位,再向上平移4个单位得到一个新的抛物线.
(1)求新的抛物线的解析式.
(2)过![]() 作直线
作直线![]() ,使得直线
,使得直线![]() 与新的抛物线仅有一个公共点,求直线
与新的抛物线仅有一个公共点,求直线![]() 的解析式及相应公共点的坐标.
的解析式及相应公共点的坐标.
(3)请猜想在新的抛物线上是否有且仅有四个点![]() 、
、![]() 、
、![]() 、
、![]() 使得
使得![]() 、
、![]() 、
、![]() 、
、![]() 分别与(2)中的所有公共点所围成的图形的面积均为S?若有,请求出S并直接写出
分别与(2)中的所有公共点所围成的图形的面积均为S?若有,请求出S并直接写出![]() 、
、![]() 、
、![]() 、
、![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com