
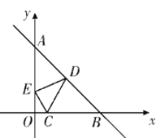
【题目】如图所示,已知点C(1,0),直线![]() 与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )
与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )
A.![]() B.10
B.10
C.![]() D.12
D.12
【答案】B
【解析】
点C关于OA的对称点C′(-1,0),点C关于直线AB的对称点C″(7,6),连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,可以证明这个最小值就是线段C′C″.
解:如图,点C(1,0)关于y轴的对称点C′(-1,0),点C关于直线AB的对称点C″,
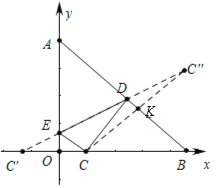
∵直线AB的解析式为y=-x+7,
∴直线CC″的解析式为y=x-1,
由![]()
解得![]() ,
,
∴直线AB与直线CC″的交点坐标为K(4,3),
∵K是CC″中点,C(1,0),
设C″坐标为(m,n),
∴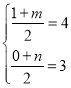 ,解得:
,解得:![]()
∴C″(7,6).
连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,
△DEC的周长=DE+EC+CD=EC′+ED+DC″=C′C″=![]()
故答案为:10.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:

①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设,企业还贷款,应每年一还,还本息,若第一年没还,则第一年的本息作为第二年的贷款本金计算. 华泰公司和宜兴公司是分别拥有96名和100名工人的小型企业,为了缓解下岗人员再就业的社会问题, 两企业2017年1月都吸收了部分下岗人员,国家对吸收下岗人员的企业贷款给予优惠,同时按季度(一年四个季度)给予企业补助,每季度补助费为:贷款总数×(吸收再就业人数÷企业原有人数)÷25 ,按两年计。华泰公司吸收了12名下岗人员,得到两年期的贷款和补助费共62.4万元资金,宜兴公司也吸收了12名下岗人员,但因贷款少,得到的补助费比华泰公司的少20%,。
(1)2017年1月华泰公司得到的贷款是多少万元?
(2)2017年1月宜兴公司得到的贷款是多少万元?
(3)假设两公司第一年都没还一分钱贷款和利息,而是两年后2019年1月才还, 宜兴公司归还贷款及利息比华泰公司少12.1万元,求国家对吸收下岗人员的企业贷款年利率.
查看答案和解析>>
科目:初中数学 来源: 题型:
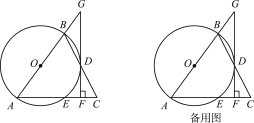
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.
(1)求证:DF是⊙O的切线;
(2)已知BD=2![]() ,CF=2,求AE和BG的长.
,CF=2,求AE和BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
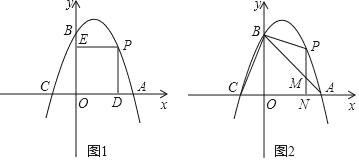
【题目】如图1,抛物线y=﹣x2+bx+c经过点A(2,0),B(0,2),与x轴交于另一点C.
(1)求抛物线的解析式及点C的坐标;
(2)点P是抛物线y=﹣x2+bx+c在第一象限上的点,过点P分别向x轴、y轴作垂线,垂足分别为D,E,求四边形ODPE的周长的最大值;
(3)如图2,点P是抛物线y=﹣x2+bx+c在第一象限上的点,过点P作PN⊥x轴,垂足为N,交AB于M,连接PB,PA.设点P的横坐标为t,当△ABP的面积等于△ABC面积的![]() 时,求t的值.
时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
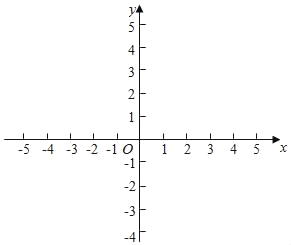
【题目】在平面直角坐标系中,抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3).
(1)求这条抛物线所对应的二次函数的表达式.
(2)直接写出该抛物线开口方向和顶点坐标.
(3)直接在所给坐标平面内画出这条抛物线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com